Вольдемар Смилга - Очевидное? Нет, еще неизведанное…

К счастью, вопрос об определении длины столь же касается геометров, как и физиков, и потому строгое математическое определение существует. (Математики не терпят никакой неопределенности.)

Определение.Длиной отрезка называется число, которое сопоставляется с каждым отрезком посредством процесса измерения.

Рецепт же для процесса измерения таков.

Чтобы измерить отрезок AB , нужно:

1) выбрать масштабный отрезок, обозначим его M (скажем, метр);

2) разбить этот отрезок на n равных между собой отрезков (допустим, 10 дециметров) — обозначим их M /n [6] Равными называются отрезки, которые можно совместить между собой путем процессов движения. Свойства движения, в свою очередь, определяются аксиомами геометрии. Возможность деления любого отрезка на два, а следовательно, и на любое число вида 2 п равных отрезков доказывается при помощи других аксиом геометрии. ;

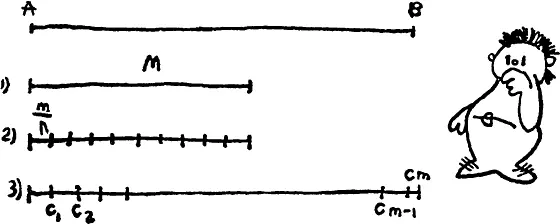
3) откладывать отрезки AC 1 = C 1 C 2 = … = C m –1 C m = M / nот точки А на отрезке AB , пока это возможно. Обозначим номер последнего m (например, 18);

4) увеличить неограниченно число n (разбивать масштабный метр на сантиметры, миллиметры и т. д.), находя каждый раз соответствующее число m (может быть, 183 см , 1834 мм …).

Предел, к которому стремится отношение m / n( 18/ 10; 183/ 100; 1834/ 1000…), и называется длиной отрезка AB , измеренного с помощью масштабного отрезка M [7] Для длины, определенной таким образом, можно доказать следующие важные теоремы: Теорема 1 . Длина всякого отрезка существует и определяется единственным образом для данного выбора масштабного отрезка. Теорема 2 . Длины равных отрезков равны. Теорема 3 . Если отрезок AC есть сумма отрезков AB и BC , то его длина равна сумме длин этих отрезков. Теорема 4 . Длина масштабного отрезка равна единице. .

Приведенное определение — типичный пример дедуктивной системы изложения — основного метода построения математики. Некоторым оно может показаться скучным и длинным, но другие, возможно, увидят в нем строгую и великолепную красоту математического мышления.

Попросту говоря, определение длины состоит в следующем.

Дайте нам масштабный отрезок, длина которого, по определению, равна единице. Откладывая его на измеряемом отрезке, мы увидим, сколько раз он уложился. Это число и есть длина измеряемого отрезка. Чтобы точно найти, сколько раз уложился масштабный отрезок на измеряемом, надо уметь откладывать и дробные доли масштаба, а значит, уметь делить масштабный отрезок на сколь угодно малые равные части. Вот и все.

Так решают вопрос математики. Но для физика и этого строгого определения недостаточно. И вот почему.

Дайте нам масштабный отрезок, говорите вы, мы его отложим вдоль измеряемого отрезка и скажем, чему равна длина. Ну, а если из-за физических условий задачи нельзя приложить масштаб? Скажем, требуется, не выезжая из Москвы, определить расстояние от Шаболовской башни до водокачки в Люберцах. Или, находясь у полотна железной дороги, не сходя с места, измерить длину проезжающего поезда. Ведь к нему масштаба не приложить. Он попросту уедет.

Далее, в процессе определения длины незримо присутствует понятие «движение». Если обратиться к геометрии, то мы будем приятно поражены, узнав, что математики считают движение понятием первичным и никак его не определяют. Физиков же это не очень устраивает.

И наконец, последнее. Математикам хорошо. Они оперируют с идеальными геометрическими отрезками. Их масштабный отрезок M не расширится при нагревании, не сократится под давлением — он обладает только геометрическими, а не физическими свойствами.

Если же мы хотим иметь строгое определение длины, пригодное для физиков, необходимо учитывать реальные свойства масштабного отрезка, а значит, сформулировать какие-то добавочные постулаты, описывающие эти свойства.

После только что сказанного может сложиться впечатление, что попытка четко определить длину и процесс ее измерения в достаточной степени безнадежна.