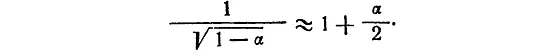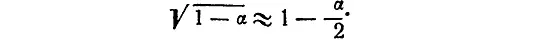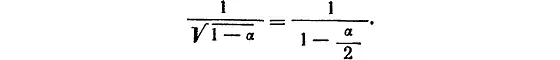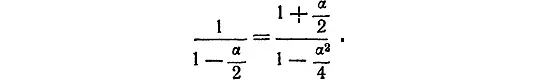Вольдемар Смилга - Очевидное? Нет, еще неизведанное…

Несущественная для нас тонкость! Если звезда находится не в плоскости эклиптики, ее видимое движение происходит по эллипсу, подобному земной орбите, как она представляется со звезды.

Между прочим, по годичному параллаксу звезды определяют ее расстояние до Земли. В наши дни параллакс определяют с точностью 0,01″. Это угол, под которым человеческий волос виден с расстояния 1,5 километра!

«Аберрация» дословно означает «отклонение», «заблуждение». Поэтому не приходится удивляться, что термин «аберрация» используют также для обозначения совершенно отличных по своей природе физических явлений, связанных с искажением хода световых лучей. Существует еще «хроматическая аберрация», «сферическая аберрация», «продольная аберрация» и еще несколько аберраций.

Орбитальная скорость Земли была известна — 30 километров в секунду.

Следует напомнить, чтó мы понимаем под неподвижным эфиром. Эфир считается покоящимся в системе неподвижных звезд.

Отношение скорости Земли к скорости света равно 30 км/сек / 3 · 10 5 км/сек = 10 –4. Тангенс такого малого угла с высокой степенью точности равен самому углу (угол измеряется в радианной мере). Поэтому

φ = v / c .

Этот эксперимент проделал, в частности, Эйри (1872 г.). Но если верить Майкельсону («Лекции по оптике»), у Эйри были предшественники, причем эксперимент был сделан, во всяком случае, до опытов Физо (1852 г.). Точную ссылку на работу Майкельсон не дает.

Например, Максвелл подметил, как из опытов Ремера можно «выловить» движение солнечной системы в целом относительно эфира уже «в первом порядке». Подробнее см.: Ландсберг , Оптика.

В первом примере. Порт — источник света. Корабль — приемник. Катера — световые волны. И наконец, море — неувлекаемый эфир.

Во втором. Корабль — источник. Порт — приемник.

Уже упоминалось, что теория неувлекаемого эфира совершенно аналогична теории распространения звуковых волн в атмосфере. Атмосфера — «неувлекаемый звуковый эфир».

Во избежание путаницы надо представлять, что поскольку (как мы увидим дальше) теория неувлекаемого эфира неправильна, неправильно и дальнейшее описание опыта.

Здесь впервые используются приближенные вычисления, на которые, несмотря на их важнейшее значение, мало обращают внимания в школе. Поэтому поясним вывод как приведенной формулы, так и еще одной, неоднократно используемой в дальнейшем.

Если α очень мало, можно утверждать, что

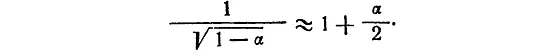
Доказать это очень просто.

Пункт № 1 . Когда α мало, то

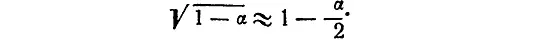
Действительно, возводя обе части приближенного равенства в квадрат, получаем 1 – α ≈ 1 – α + α 2/4.

Правая часть равенства больше левой на α 2/4, но если α << 1, то α 2совсем уже малая величина и ею можно пренебречь (если, например, α = 0,001, α 2 = 0,000001).

Итак, с точностью до членов порядка α 2,

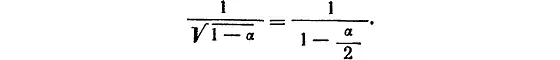
Пункт № 2. Умножим числитель и знаменатель дроби 1/(1 – α/ 2) на 1 + α/ 2. Получим, что

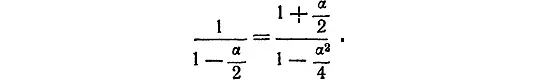
Как и раньше, можно пренебречь членом α 2/4 в знаменателе. Тогда окончательно

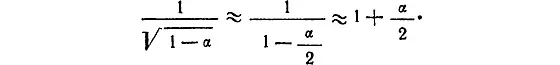
Это равенство справедливо с точностью до членов порядка α 2. Не следует опасаться, конечно, того, что мы пренебрегали членами порядка α 2не один, а два раза. Это не может сколько-нибудь заметно увеличить ошибку.

Фактически невозможно уловить разницу между тысячью человек, тысячью без одного или же тысячью без двух.

Так как v Земли = 30 км/сек., то v Земли/ C = 10 –4и ( t N1 – t N2) = t 0 v 2/2 c 2 = t 0/2 · 10 –8.

Теплород, флогистон, horror vacui (ужас пустоты) — все это в свое время очень модные и распространенные теоретические концепции, отброшенные в дальнейшем как несостоятельные.