Олег Спиридонов - Людвиг Больцман - Жизнь гения физики и трагедия творца

Дальнейшее развитие атомистической гипотезы было небезмятежным. В 1808 г. французский ученый Ж. Л. Гей-Люссак открыл закон объемных отношений, согласно которому объемы как участвующих в реакции газов, так и газообразных продуктов реакции находятся в простых кратных отношениях. Это противоречило теории Дальтона, в которой соединялись равные количества атомов, и… Дальтон отказывается признавать закон Гей-Люссака. Но один-единственный факт, не укладывающийся в какую-либо теорию, способен опровергнуть ее.

После открытия Гей-Люссака судьба всей атомной теории вызвала сомнения.

«Существует огромная разница между фантазиями натурфилософов, легкомысленно сбивающихся с пути опыта, и надежными выводами теоретической физики, медленно и методически продвигающейся вперед пол непрестанным контролем эксперимента. Последняя позволяет проникать глубоко в тайны природы, не теряя надежной почвы пол ногами, и в этом она достигает своих высших триумфов».

Блестящим подтверждением этих слов может служить гениальная идея итальянского ученого А. Авогадро (1776-1856). В 1811 г. он указал на возможность создания новой теории, объединяющей две существующие теории — Дальтона и Гей-Люссака. Авогадро вводит в науку о строении вещества понятие молекулы — соединения атомов. Удивительное предвидение! Еще под вопросом реальность атомов, а результаты исследований требуют объяснения и находят его в созданной Авогадро молекулярной теории строения вещества.

Важнейшим следствием гипотезы Авогадро является закон, имеющий громадное теоретическое значение, — при одинаковых температуре и давлении равные объемы любых газов содержат одно и то же число молекул! Этот вывод закреплял в науке представление о дискретном, зернистом, строении вещества. Используя данные опытов Дальтона и Гей-Люссака, Авогадро возводит удивительно стройное «молекулярное здание», предсказывая новые, уникальные факты.

Из гипотезы Авогадро вытекает существование постоянного числа молекул в моле [2] Моль — количество вещества, содержащее столько же молекул или атомов, сколько содержится атомов в углероде массой 0,012 кг. любого вещества. Объем V 0, который занимает моль любого газа при нормальных условиях, также является постоянным. Этот объем был измерен экспериментально:

Одной из самых первоначальных задач науки стало определение числа молекул N Aв 1 моле любого вещества, получившего в дальнейшем название постоянной Авогадро. Зная V 0и N A, мы можем рассчитать важнейшие характеристики атомов — их массы, размеры, среднее расстояние между атомами в газах. Выполним эти расчеты.

Предположим, что постоянная Авогадро нам известна (о способах ее определения можно узнать в школьных учебниках физики):

Поскольку масса одного моля водорода равна 2,016 г и в нем содержится N A молекул, то масса одной молекулы водорода будет равна m H2= 3,35∙10 -24г, а масса одного атома m H= 1,675∙10 -24г. Поразительно могущество теории — мы «взвесили» атом водорода, не прибегая к помощи весов (да и возможны ли весы, способные взвешивать столь ничтожные тела?).

Оценим размеры атомов. Объем воды, равный 1 см 3, составляет 1/18 часть моля, поэтому в нем содержится 3,34∙10 22молекул. Объем, приходящийся на одну молекулу воды, равен (1/3,34)∙10 22см 3, т.е. примерно 3∙10 -23см 3. Предполагая, что молекулы расположены плотно друг к другу, оценим линейные размеры молекул воды:

Размеры других атомов и простейших молекул — этого же порядка.

Расстояние между молекулами в газах можно оценить следующим образом:

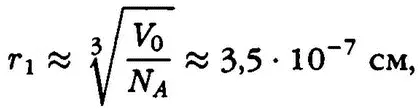
т. е. молекулы в газах находятся друг от друга на расстояниях, примерно в 10 раз больших, чем их собственные размеры.

Введение в химию атомистических представлений позволило ученым добиться несомненных успехов в познании строения вещества, но и поставило перед ними множество трудных вопросов. К открытому Бойлем и Мариоттом закону pV = const спустя почти 150 лет добавился закон Гей-Люссака, связывающий относительное изменение объема газа и его температуру T:

где α — коэффициент термического расширения газов, равный 1/273 К -1. Вскоре французский ученый Э. Клапейрон связал воедино все три параметра газа и получил уравнение состояния идеального газа, которое носит название уравнения Клапейрона: