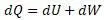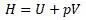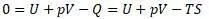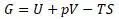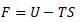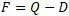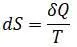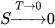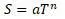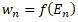Константин Ефанов - Вопросы теоретической термодинамики

Рассмотрим уравнение Клазиуса

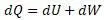
Уравнение энтальпии по структуре соответсвует этому уравнению и оно получается заменой выражений в этом уравнении, то есть:

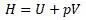
Но уравнение энергии Гиббса состоит из 4 слагаемых.

Перепишем уравнение Клазиуса:

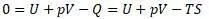
Так получена структура уравнения энергии Гиббса, обозначенная «G» c введением четвертого слагаемого. И эта функция не равна нулю в общем случае.

Такая структура показывает сильное отличие от структуры уравнения Гельмгольца при W=0.

В формуле энергии Гиббса и уравнении Клазиуса энергия «U» обозначает одинаковую физическую величину. При том, что для случая уравнения Гельмгольца и Клазиуса имеется несоответствие (см. соотв. параграф).

Сравним структуры формул Гиббса и Гельмгольца:

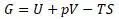
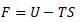
По виду уравнений, отличие состоит на первый взгляд в слагаемом «pV».

Однако, в уравнении Гельмгольца энтропийный член соответствует связанной энергии D из соображения Гельмгольца по делению энергии на связанную и свободную. А в уравнении Гиббса энтропийный член соответствует величине Q из уравнения Клазиуса. И как было показано выше, эти две величины отличаются на величину:

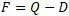
То есть, можно сделать вывод, что уравнения Гиббса и Гельмгольца имеют отличия в слагаемом TS, в величине энтропийного члена. Вместе с тем из сравнения структур этого нельзя сразу установить. Потребуется прочитать параграф, касающийся энергии Гельмгольца.

Уравнения для сравнительного прочтения можно представить в форме:

В записи в такой форме видна разница между физическим смыслом энергий «U» и энергий в тепловой связанной форме «Q» и «D».

Такое различие имеет следующее обоснование:

– Клазиус ввел понятие внутренней энергии, содержащей теплосодержание (термин схож с применяемым для энтальпии) U = H + J;

– Гельмгольц разделил энергию системы на свободную и связанную. Полная энергия Гельмгольца не равна энергии Клазиуса с тем же обозначением «U»: U = F + D;

– Энтальпия получается из уравнения Клазиуса,

– Свободная энергия Гиббса получается на основании уравнения энтальпии, а, следовательно, и уравнения Клазиуса.

– Отличия в уравнениях Клазиуса и Гельмгольца переходят в отличия между уравнениями Гиббса и Гельмгольца.

В рамках квантовой статистики получена теорема Нернста, состоящая в том, что при абсолютном нуле энтропия равна нулю. В классической статистике такой результат не может быть получен так как энтропия вычисляется до аддитивной постоянной:

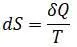
Формулировка теоремы Нернста:

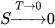
При снижении температуры тело будет иметь состояние с минимальной энергией, в основном квантовом состоянии.

Статистический вес макроскопического состояния тела равен 1 и энтропия как логарифм 1 равна 0.

Энтропия обращается в 0 по степенному закону

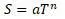
На степенных законах основаны термодинамические расчеты по уравнениям:

Система делится на подсистемы с функцией распределения w n.

Функция распределения является функцией энергии:

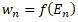
Находят вероятность энергии между E и (E + dE). Для этого обозначают через dГ число с вероятностью равной или меньше Е.

Распределение энергии по вероятности:

Площадь под кривой равна 1, т.е.:

Для кривой вводят прямоугольник с шириной ΔЕ, высота которого равна максимому кривой при площади равной 1:

Перепишем уравнение для W(E):

Число квантовых состояний:

Выполняется переход от квантовой статистики к классической статистике:

(s – число степеней свободы, ΔpΔq – фазовый объем, 2πℏ – объем клетки в фазовом пространстве)

Энтропией подсистемы является логарифм величины ΔГ:

Энтропия положительная так как число состояний ΔГ больше 1.

В классической статистике энтропия определяется до аддитивной постоянной так как lndpdq имеет физическую размерность действия. При этом разность энтропий не зависит от выбора единиц.