Мичио Каку - Уравнение Бога. В поисках теории всего

Это повергло физиков в настоящий шок, поскольку прежде никто ничего подобного не видел. Обычно теорию можно выразить в любой размерности, какая вам нравится. Мы просто отбрасываем все остальные варианты, потому что живем – со всей очевидностью – в трехмерном мире. (Мы можем двигаться только вперед-назад, вправо-влево и вверх-вниз. Если добавить время, то четырех измерений вполне хватит, чтобы определить местонахождение любого события во Вселенной. Если, например, мы хотим встретиться с кем-то на Манхэттене, то достаточно сказать: давай встретимся на углу 5-й авеню и 42-й улицы, на десятом этаже, в полдень. Движение в измерениях сверх этих четырех для нас невозможно, как бы мы ни старались. Мало того, наш мозг не способен даже представить зрительно, каково это – двигаться в более высоких измерениях. Поэтому исследования многомерной теории струн проводятся исключительно математически.)

Но в теории струн размерность пространства-времени имеет фиксированные десять измерений. В других размерностях теория математически рушится.

Я до сих пор помню шок, который испытали физики, когда теория струн вдруг постулировала, что мы живем в десятимерной вселенной. Большинство физиков увидели в этом доказательство ошибочности теории. Когда Джон Шварц, один из ведущих архитекторов теории струн, сталкивался в лифте Калтеха с Ричардом Фейнманом, тот частенько поддевал его, обращаясь с вопросом: «Ну, Джон, в скольких измерениях вы сегодня находитесь?»

Тем не менее с годами физики начали показывать, что все конкурирующие теории страдают фатальными недостатками. Например, многие из них можно было исключить просто потому, что в них квантовые поправки оказывались бесконечными или аномальными (то есть математически противоречивыми).

Так что со временем физики начали свыкаться с идеей, что наша Вселенная, возможно, все-таки десятимерна. Наконец в 1984 г. Джон Шварц и Майкл Грин показали, что теория струн свободна от всех тех проблем, что обрекали на неудачу прочих претендентов на роль единой теории поля.

Если теория струн верна, то вселенная, возможно, изначально была десятимерной. Но такая вселенная оказалась нестабильной, и шесть измерений из десяти каким-то образом свернулись и стали слишком маленькими, чтобы их можно было увидеть. Из этого следует, что на самом деле наша Вселенная, возможно, десятимерна, но атомы слишком велики, чтобы проникнуть в эти крохотные высшие измерения.

Несмотря на все безумие струнной теории, одна ее способность не дает ей сойти со сцены: она успешно «сочетает браком» две великие физические теории – общую теорию относительности и квантовую теорию – и, таким образом, дарует нам конечную теорию квантовой гравитации. Именно этим объясняется ажиотаж вокруг теории струн.

Как уже говорилось, добавляя к КЭД квантовые поправки или частицу Янга – Миллса, мы получаем поток расходимостей, которые необходимо устранять.

Но все это ни к чему не приводит, если мы пытаемся устроить вынужденный брак двух великих теорий природы – теории относительности и квантовой теории. Чтобы применить квантовый принцип к гравитации, мы разбиваем ее на энергетические пакеты, или кванты, называемые гравитонами. Затем мы рассчитываем столкновение гравитонов друг с другом и с частицами материи, такими как электрон. Но при этом весь набор фокусов, придуманных Фейнманом и 'тХоофтом, не дает результата. Квантовые поправки, вызванные взаимодействием гравитонов с другими гравитонами, расходятся и совершенно не поддаются устранению методами, найденными предыдущими поколениями физиков.

Вот здесь-то и происходит следующий акт волшебства. Теория струн в состоянии устранить эти проблематичные расходимости, донимавшие физиков на протяжении почти столетия. И это волшебство вновь реализуется через симметрию.

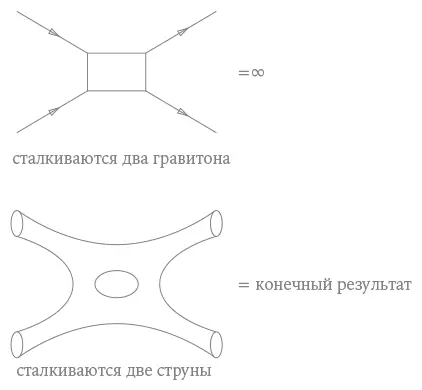
Рис. 11.При расчете столкновения двух гравитонов ( вверху ) ответ получается бесконечным, а значит, бессмысленным. Но когда сталкиваются две струны ( внизу ), мы получаем два слагаемых – одно от бозонов, другое от фермионов. В теории струн два этих слагаемых в точности компенсируют друг друга, помогая создать конечную теорию квантовой гравитации

Исторически симметричность уравнений считалась положительным качеством, но рассматривалась как роскошь, в которой не было строгой необходимости. В квантовой теории симметрия становится самым важным свойством физики.