Если результат расчета будет выражен в векторной записи, то можно говорить, что он не зависит от специальной ориентации плоскости.
Мы хотим теперь найти циркуляцию поля Спо нашему квадратику. Криволинейное интегрирование легко проделать, если квадратик сделать таким маленьким, чтобы вектор Сна протяжении одной стороны квадрата менялся очень мало. (Это предположение выполняется тем лучше, чем меньше квадратик, так что на самом деле речь идет о бесконечно малых квадратиках.) Отправившись от точки ( х, у ) — в левом нижнем углу фигуры,— мы обойдем весь квадрат в направлении, указанном стрелками. Вдоль первой стороны, отмеченной цифрой 1, касательная составляющая равна С х (1), а расстояние равно Δх. Первая часть интеграла равна C x(1) Δх. Вдоль второй стороны получится С у(2) Δy. Вдоль третьей мы получим -С x(3) Δх, а вдоль четвертой -C y(4) Δy. Знаки минус стоят потому, что нас интересует касательная составляющая в направлении обхода. Весь криволинейный интеграл тогда равен
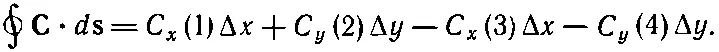 (3.31)
(3.31)
Посмотрим теперь на первый и третий члены. В сумме они дают
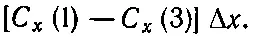 (3.32)
(3.32)
Вам может показаться, что в принятом приближении эта разность равна нулю. Но это только в первом приближении. Мы можем быть более точными и учесть скорость изменения С х , тогда можно написать
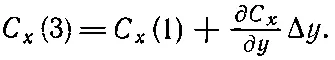 (3.33)
(3.33)
В следующем приближении пойдут члены с (Δy) 2, но ввиду того, что нас интересует в конечном счете только предел при Δy→0, то этими членами можно пренебречь. Подставляя (3.33) в (3.32), мы получаем
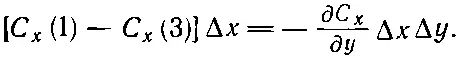 (3.34)
(3.34)
Производную при нашей точности можно брать в точке ( х, у ). Подобным же образом оставшиеся два члена можно написать в виде
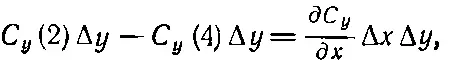 (3.35)
(3.35)
и циркуляция по квадрату тогда равна
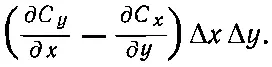 (3.36)
(3.36)
Интересно, что в скобках получилась как раз z-компонента ротора С . Множитель ΔxΔy— это площадь нашего квадрата. Так что циркуляцию (3.36) можно записать как
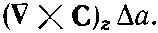
Но z-компонента это на самом деле компонента, нормальная к элементу поверхности. Поэтому циркуляцию вокруг квадратика можно задать и в инвариантной векторной записи:
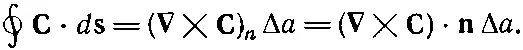 (3.37)
(3.37)
В результате имеем: циркуляция произвольного вектора Спо бесконечно малому квадрату равна произведению составляющей ротора С, нормальной к поверхности, на площадь квадрата.
Циркуляция по произвольному контуру Γ легко теперь может быть увязана с ротором векторного поля. Натянем на контур любую подходящую поверхность S (как на фиг. 3.11) и сложим между собой циркуляции по всем бесконечно малым квадратикам на этой поверхности.
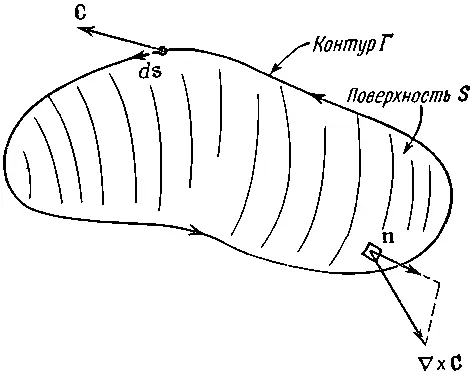
Фиг. 3.11. Циркуляция вектора С по Γ равна поверхностному интегралу от нормальной компоненты вектора ∇×С.
Сумма может быть записана в виде интеграла. В итоге получится очень полезная теорема, называемая теоремой Стокса [по имени физика Стокса].
ТЕОРЕМА СТОКСА
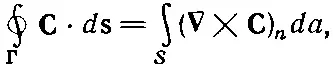 (3.38)
(3.38)
где S — произвольная поверхность, ограниченная контуром Γ. Теперь мы должны ввести соглашение о знаках. На приведенной ранее фиг. 3.10 ось z показывает на вас, если система координат «обычная», т. е. «правая». Когда в криволинейном интеграле мы брали «положительное» направление обхода, то циркуляция получилась равной z-компоненте вектора ∇× C. Обойди мы контур в другую сторону, мы бы получили противоположный знак. Как вообще узнавать, какое направление надо выбирать для положительного направления «нормальной» компоненты вектора ∇× C? «Положительную» нормаль надо всегда связывать с направлением так, как это сделано было на фиг. 3.10. Общий случай показан на фиг. 3.11.
Читать дальше

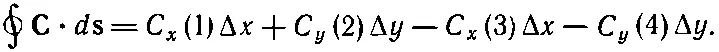 (3.31)
(3.31)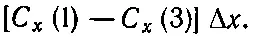 (3.32)
(3.32)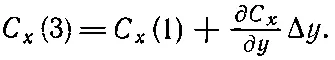 (3.33)
(3.33)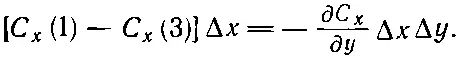 (3.34)
(3.34)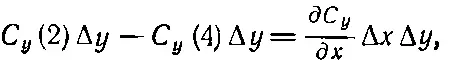 (3.35)
(3.35)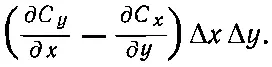 (3.36)
(3.36)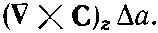
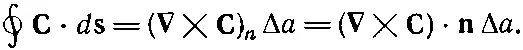 (3.37)
(3.37)
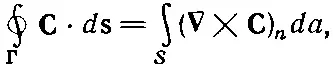 (3.38)
(3.38)



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)


