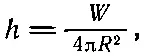
или
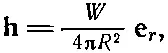 (3.24)
(3.24)
где, как всегда, e rобозначает единичный вектор в радиальном направлении. Этот результат говорит нам, что hпропорционален W и меняется обратно квадрату расстояния от источника.
Только что полученный результат применим к потоку тепла вблизи точечного источника тепла. Теперь попытаемся найти уравнения, которые справедливы для теплового потока самого общего вида (придерживаясь единственного условия, что количество тепла должно сохраняться). Нас будет интересовать только то, что происходит в местах вне каких-либо источников или поглотителей тепла.
Дифференциальное уравнение распространения тепла было получено в гл. 2. В соответствии с уравнением (2.44),
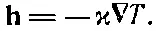 (3.25)
(3.25)
(Помните, что это соотношение приближенное, но для некоторых веществ вроде металлов выдерживается неплохо.) Применимо оно, конечно, только в тех частях тела, где нет ни выделения, ни поглощения тепла. Выше мы вывели другое соотношение (3.21), которое выполняется тогда, когда количество тепла сохраняется. Если мы это уравнение скомбинируем с (3.25), то получим
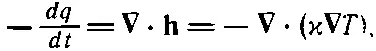
или
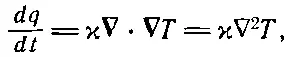 (3.26)
(3.26)
если ϰ — величина постоянная. Напоминаю, что q — это количество тепла в единичном объеме, а ∇· ∇=∇ 2— лапласиан, т. е. оператор
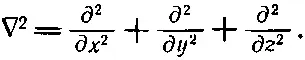
Если мы теперь сделаем еще одно допущение, сразу возникнет одно очень интересное уравнение. Допустим, что температура материала пропорциональна содержанию тепла в единице объема, т. е. что у материала есть определенная удельная теплоемкость. Когда это допущение верно (а так бывает часто), мы можем писать
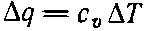
или
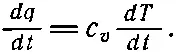 (3.27)
(3.27)
Скорость изменения количества тепла пропорциональна скорости изменения температуры. Коэффициент пропорциональности c v здесь — удельная теплоемкость на единицу объема материала. Подставляя (3.27) в (3.26), получаем
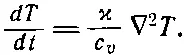 (3.28)
(3.28)
Мы обнаружили, что быстрота изменения со временем температуры Т в каждой точке пропорциональна лапласиану от Т , т. е. вторым производным от пространственного распределения температур. Мы имеем дифференциальное уравнение — в переменных х, у, z и t — для температуры Т .
Дифференциальное уравнение (3.28) называется уравнением диффузии тепла , или уравнением теплопроводности . Часто его пишут в виде
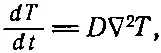 (3.29)
(3.29)
где D — постоянная. Она равна ϰ/c v.
Уравнение диффузии появляется во многих физических задачах: о диффузии газов, диффузии нейтронов и других. Мы уже обсуждали физику некоторых таких явлений в вып. 4, гл. 43. Теперь перед вами полное уравнение, описывающее диффузию в самом общем виде. Немного позже мы займемся решением уравнения диффузии, чтобы посмотреть, как распределяется температура в некоторых случаях. А сейчас вернемся к рассмотрению других теорем о векторных полях.
§ 5. Циркуляция векторного поля
Мы хотим теперь рассмотреть ротор поля примерно так же, как рассматривали дивергенцию. Мы вывели теорему Гаусса, вычисляя интеграл по поверхности, хотя с самого начала отнюдь не было ясно, что мы будем иметь дело с дивергенцией. Откуда же можно было знать, что для ее получения надо интегрировать по поверхности? Этот результат вовсе не был очевиден. И столь же неоправданно мы сейчас вычислим другую характеристику поля и покажем, что она связана с ротором. На этот раз мы подсчитаем так называемую циркуляцию векторного поля. Если С— произвольное векторное поле, мы возьмем его составляющую вдоль кривой линии и проинтегрируем эту составляющую по замкнутому контуру. Интеграл называется циркуляцией векторного поля по контуру. Мы уже раньше в этой главе рассматривали криволинейный интеграл от ∇ψ. Сейчас мы то же самое проделываем с произвольным векторным полем С.
Читать дальше

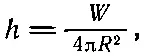
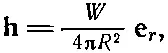 (3.24)
(3.24)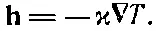 (3.25)
(3.25)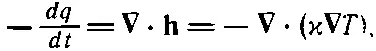
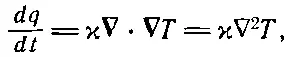 (3.26)
(3.26)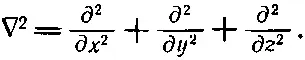
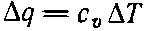
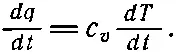 (3.27)
(3.27)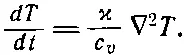 (3.28)
(3.28)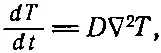 (3.29)
(3.29)



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)


