Предположим, что нужно собрать более сложную цепь из двух кусков, импедансы которых равны ^Z 1и ^Z 2; соединим их последовательно (фиг. 25.6, а) и приложим напряжение.
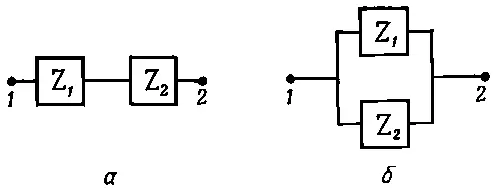
Фиг. 25.6. Импедансы, соединенные последовательно (а) и параллельно (б).
Что случится? Задача немного сложнее предыдущей, но разобраться в ней нетрудно: если через Z 1течет ток ^ I 1, то падение напряжения на ^Z 1равно ^ V 1=^ I ^ Z 1, а падение напряжения на ^Z 2будет ^ V 2=^ I ^ Z 2. Через оба элемента цепи течет одинаковый ток . Полное падение напряжения вдоль такой цепи равно ^V=^V 1+^V 2=(^Z 1+^Z 2)I. Таким образом, падение напряжения в такой цепи мощно записать в виде ^V=^I^Z s, а ^ Z s — импеданс системы, составленной из двух последовательно соединенных элементов, равен сумме импедансов отдельных элементов
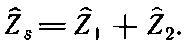 (25.16)
(25.16)
Но это не единственный способ решения вопроса. Можно соединить отдельные элементы параллельно (фиг. 25.6,б). При таком соединении, если соединительные провода считать идеальными проводниками, к обоим элементам приложено одинаковое внешнее напряжение, а сила тока в каждом элементе не зависит от другого элемента. Ток через ^Z 1равен ^I 1=^V/^Z 1, ток в ^Z 2равен ^I 2=^V/^Z 2. Напряжение в обоих случаях одинаково . Полный ток через концы цепи равен сумме токов в отдельных частях цепи: ^I=^V/^Z 1+^V/^Z 2. Это можно записать и так:
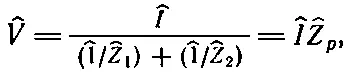
Таким образом,
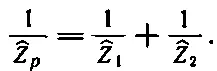 (25.17)
(25.17)
Многие сложные цепи иногда становятся более понятными, если расчленить их на куски, выяснить, чему равны импедансы отдельных частей, а затем шаг за шагом следить за соединением частей, помня о только что выведенных правилах. Если мы собрали цепь из большого числа произвольно соединенных элементов и создаем в этой цепи разности потенциалов при помощи небольших генераторов, импедансом которых можно пренебречь (когда заряд проходит через генератор, то потенциал возрастает на V), то при анализе цепи можно использовать такие правила:
1) сумма токов, протекающих через любое соединение, равна нулю; ведь притекший к любому соединению ток должен обязательно вытечь из него;
2) если заряд, двигаясь по замкнутой петле, вернулся в то место, откуда начал путешествие, полная работа должна быть равна нулю.
Эти правила называются законами Кирхгофа . Систематическое применение этих правил часто облегчает анализ работы сложных цепей. Мы к ним вернемся, когда будем говорить о законах электричества.
Выпуск 3. Излучение. Волны. Кванты
Глава 26 ОПТИКА. ПРИНЦИП НАИМЕНЬШЕГО ВРЕМЕНИ
Эта глава — первая из посвященных электромагнитному излучению. Свет, с помощью которого мы видим, составляет только небольшую часть широкого спектра явлений одной природы, причем разные части спектра характеризуются разными значениями определенной физической величины. Эту величину называют «длиной волны». По мере того, как она пробегает значения в пределах спектра видимого света, цвет световых лучей меняется от красного до фиолетового. Систематическое изучение спектра от длинных волн к коротким лучше всего начать с так называемых радиоволн. В технике радиоволны получают в широком диапазоне длин волн и даже более длинные, чем те, которые используются в обычном радиовещании. В радиовещании применяются волны длиной около 500 м , за ними идут так называемые короткие волны, далее радиолокационный диапазон, миллиметровый диапазон и т. д. На самом деле между разными диапазонами нет никаких границ, природа их не создала. Числа, которые соответствуют разным диапазонам, и, конечно, сами названия диапазонов весьма условны.
Далее, пройдя долгий путь через миллиметровый диапазон, мы придем к инфракрасным волнам, а оттуда к спектру видимого света. Спустившись за его границы, мы попадем в ультрафиолетовую область. За ультрафиолетовой областью начинаются рентгеновские лучи, но границу между ними точно определить мы не можем, она где-то около 10 -8 м , или 10 -2 мк . Это область мягких рентгеновских лучей, за нею идет обычное рентгеновское излучение, затем жесткое излучение, потом γ-излучение и так ко все меньшим значениям величины, которую мы назвали длиной волны.
Читать дальше

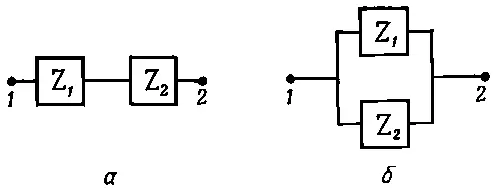
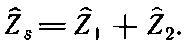 (25.16)
(25.16)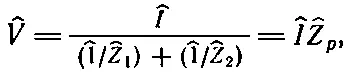
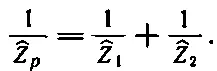 (25.17)
(25.17)




