* * *
Теперь Мик подсчитывает моменты сил в своей системе.
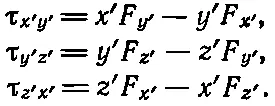 (20.2)
(20.2)
Пусть одна система координат повернута на угол θ по отношению к другой, так что ось z осталась той же самой. (Угол θ ничего не имеет общего с вращением объекта или с чем-то происходящим внутри системы координат. Это просто связь между осями, используемыми одним человеком, и осями, используемыми другим. Мы предполагаем, что он остается постоянным.) При этом координаты в двух системах связаны так:
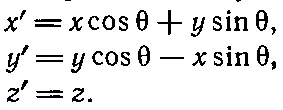 (20.3)
(20.3)
Точно таким же образом, поскольку сила является вектором, она преобразуется в новой системе координат так же, как x, y и z. Просто, по определению, объект называется вектором тогда и только тогда, когда различные его компоненты преобразуются как x, y и z
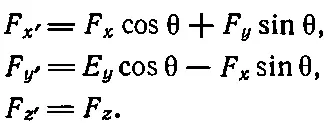 (20.4)
(20.4)
Теперь можно определить, как преобразуется момент силы. Для этого в уравнение (20.2) нужно просто подставить вместо х ', у ' и z ' выражение (20.3), а для F x ', F y ', и F z '-— выражение (20.4). В результате для τ x'y'получается длинный ряд членов, но оказывается (и на первый взгляд это удивительно), что все сводится просто к выражению xF y - yF x , которое, как известно, является моментом силы в плоскости ху :
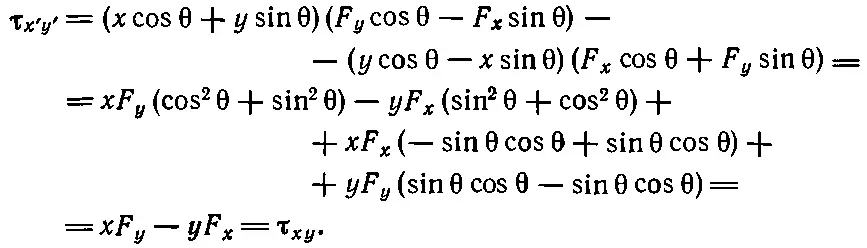 (20.5)
(20.5)
Результат совершенно ясен: ведь мы только повернули оси, лежащие в плоскости ху , при этом момент относительно оси z в этой плоскости не отличается от прежнего: ведь плоскость-то осталась той же самой! Более интересно выражение для τ V ' Z '. Здесь уже мы имеем дело с новой плоскостью. Если теперь повторить то же самое с плоскостью y ' z ', то получим
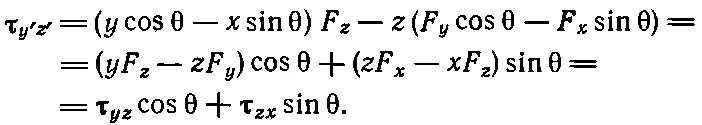 (20.6)
(20.6)
И наконец, для плоскости z ' x '
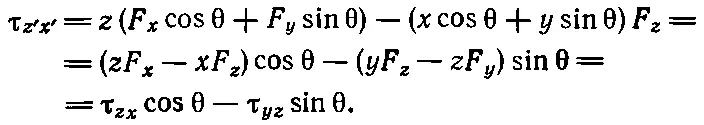 (20.7)
(20.7)
Мы хотели найти правило для определения момента сил в новой системе через момент сил в старой и нашли его. Как можно запомнить это правило? Если внимательно посмотреть на уравнения (20.5)—(20.7), то нетрудно увидеть, что между ними и уравнениями для x, y и z существует тесная связь. Если каким-то образом мы бы могли назвать τ xу z-компонентой чего-то, скажем z-компонентой вектора τ, то все было бы в порядке: уравнение (20.5) мы бы понимали как преобразование вектора τ, ибо z-компонента его, как это и должно быть, оставалась бы неизменной. Аналогично, если связать плоскость yz с x- ком понентой новоиспеченного вектора, а плоскость zx с у - компо нентой, то закон преобразования будет выглядеть так:
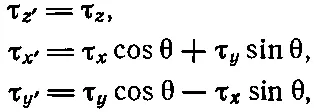 (20.8)
(20.8)
что в точности соответствует закону преобразования векторов.
Мы, следовательно, доказали, что комбинацию xF y - yF x можно отождествить с тем, что обычно называется z-компонентой некоторого искусственно введенного вектора. Хотя момент сил является своего рода «кручением» в плоскости и, казалось бы, не имеет векторного характера, математически он все-таки ведет себя как вектор. Этот вектор направлен под прямым углом к плоскости кручения, а его длина пропорциональна силе кручения. Три компоненты такой величины будут преобразовываться при вращении как самый настоящий вектор.
Итак, мы представляем момент силы в виде вектора. Согласно правилу, с каждой плоскостью, в которой он действует, мы связываем прямую, перпендикулярную к этой плоскости. Однако перпендикулярность к плоскости оставляет неопределенный знак вектора. Чтобы определить его, необходимо еще одно дополнительное правило, которое говорило бы нам, что если момент силы действует определенным образом в плоскости ху , то соответствующий ему вектор направлен «вверх» по оси z. Это означает, что предварительно кто-то должен сказать нам, где «право», а где «лево». Предположим, что система координат xyz правосторонняя; тогда правило должно быть таким: если представить себе кручение как ввертывание болта с правовинтовой резьбой, то направление вектора, связанного с этим кручением, определяется поступательным движением болта.
Читать дальше

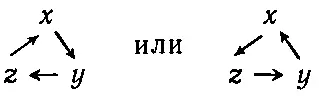
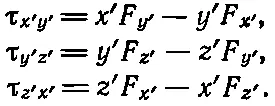 (20.2)
(20.2)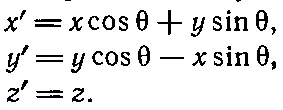 (20.3)
(20.3)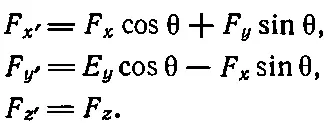 (20.4)
(20.4)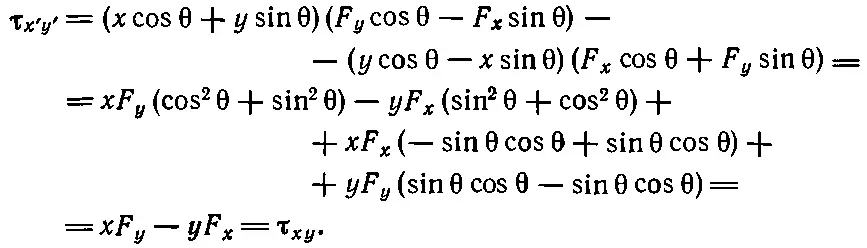 (20.5)
(20.5)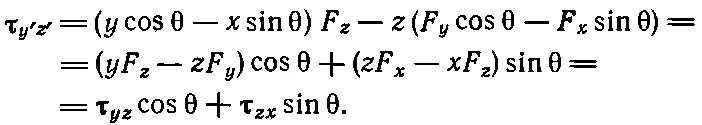 (20.6)
(20.6)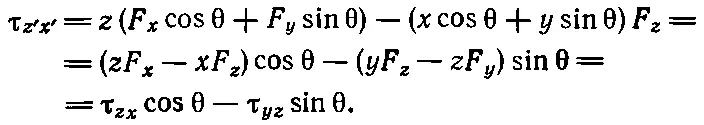 (20.7)
(20.7)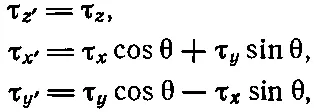 (20.8)
(20.8)




