В этих рассуждениях кроется ключ к вычислению силы или напряженности поля, когда потенциальная энергия известна.
Пусть потенциальная энергия тела в точке ( x, y, z ) дана, а мы хотим узнать, какая сила действует на него в этой точке. Для этого нужно знать потенциал не только в этой точке, но и в соседних. Почему? Попробуем вычислить x -компоненту силы (если мы это сумеем сделать, то точно таким же способом мы вычислим и у - и z -компоненты, определив тем самым всю силу). Если б мы сдвинули тело на малое расстояние Δ x , то работа, произведенная силой над телом, равнялась бы x -компоненте силы, умноженной на Δ x (если Δ x достаточно мало), и должна была бы быть равна изменению потенциальной энергии при переходе от одной точки к другой:
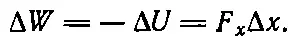 (14.9)
(14.9)
Мы просто применили формулу ∫ F· d s=-Δ U для очень малых расстояний. Теперь разделим на Δ x и обнаружим, что сила равна
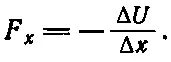 (14.10)
(14.10)
Конечно, это не совсем точно. На самом деле нам нужно перейти в (14.10) к пределу при Δ x , стремящемся к нулю, потому что (14.10) точно соблюдается только для бесконечно малых Δx. Мы узнаем в правой части (14.10) производную U по х и хотим написать - dU / dx . Но U зависит и от х , и от у , и от z, и для такого случая математики придумали другое обозначение, которое рассчитано на то, чтобы напоминать нам, что надо быть очень осторожным, дифференцируя такую функцию. Этот символ напоминает, что только х считается изменяющимся, а у и z — нет. Вместо d они просто пишут «6 навыворот», или ∂. (По-моему, когда начинаешь изучать дифференциальные исчисления, то вообще лучше работать с ∂, а не с d ; d всегда хочется сократить, а вот на ∂ как-то рука не поднимается!) Итак, они пишут ∂ U /∂ x , а иногда в припадке строгости, желая быть очень бдительными, они ставят за ∂ х скобку с маленькими у, z внизу (∂ U /∂ x ) yz , что означает: «Продифференцируй U по х , считая у и z постоянными». Но мы чаще всего не будем отмечать, что осталось постоянным, из контекста это всегда можно понять. Но зато всегда будем писать ∂ вместо d как предупреждение о том, что эта производная берется при постоянных значениях прочих переменных. Ее называют частной производной , т. е. производной, для вычисления которой меняют часть переменных, х .
Итак, мы обнаруживаем, что сила в направлении х равна минус частной производной U по х :
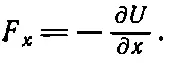 (14.11)
(14.11)
Точно так же и сила в направлении у получается дифференцированием U по у при постоянных х и z, а третья составляющая силы опять-таки есть производная по z при х и у постоянных:
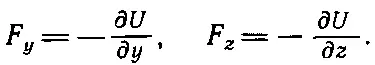 (14.12)
(14.12)
В этом и состоит способ получать силу из потенциальной энергии. Поле получается из потенциала в точности так же:
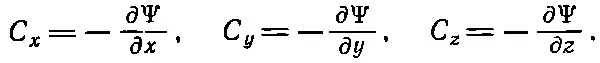 (14.13)
(14.13)
Заметим, кстати, что существует и другое обозначение (впрочем, пока оно нам не понадобится). Так как Сесть вектор с компонентами x, y, z , то символы ∂/∂ х , ∂/∂ y , ∂/∂ z , дающие х -, у -, z-компоненты поля, чем-то напоминают векторы. Математики изобрели знаменитый символ ∇, или grad, называемый «градиентом»; это не величина, а оператор, он делает из скаляра вектор. У него есть три составляющие: x-компонента этого grad есть ∂/∂ x , y-компонента — ∂/∂ y , а z-компонента — ∂/∂ z , и мы можем позабавиться, переписав наши формулы в виде
 (14.14)
(14.14)
Глядя на ∇; мы мгновенно узнаем, что наши уравнения векторные; но на самом деле уравнение (14.14) означает в точности то же, что и (14.11) и (14.12); просто это другой способ записи. Не желая писать каждый раз три уравнения, мы пишем одно лишь ∇ U .
Читать дальше

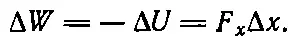 (14.9)
(14.9)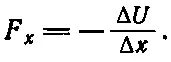 (14.10)
(14.10)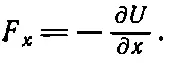 (14.11)
(14.11)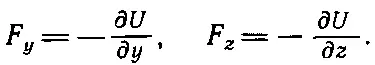 (14.12)
(14.12)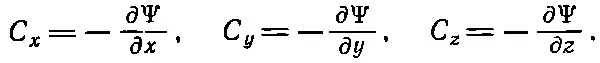 (14.13)
(14.13) (14.14)
(14.14)




