Обозначим эту функцию положения через - U ( x, у, z ); желая отметить, что речь идет именно о точке 2 с координатами x 2, y 2, z 2, мы будем просто писать U (2), сокращая обозначение U( х 2, у 2, z 2). Работу перемещения из точки 1 в точку Р можно написать, обратив направление интегрирования (переменив знаки всех d s). Другими словами, работа на участке (1, Р ) равна работе на участке ( P ,1) со знаком минус:
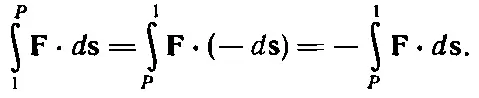
Значит, работа на участке ( Р ,1) есть - U (1), а на участке ( Р ,2) есть - U (2). Поэтому интеграл от 1 до 2 равен - U (2) плюс [- U (1) назад], т. е. + U (1)- U (2):
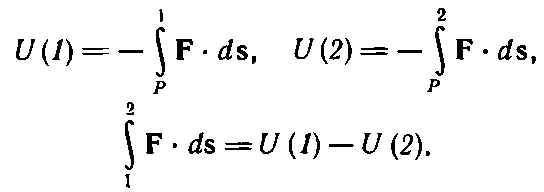 (14.1)
(14.1)
Величина U (1)- U (2) называется изменением потенциальной энергии, а U можно назвать потенциальной энергией. Мы будем говорит, что когда предмет находится в положении 2, то он обладает потенциальной энергией U (2), а в положении 1 — потенциальной энергией U (1). Когда он находится в положении Р, его потенциальная энергия равна нулю. Если бы вместо Р взять любую другую точку Q , то оказалось бы (это предоставляется доказать вам самим), что потенциальная энергия всех точек изменилась бы только на постоянную добавку . Так как сохранение энергии зависит только от изменений ее, то эта добавочная постоянная никакого значения не имеет. Вот поэтому точка Р произвольна.
Итак, у нас имеются два утверждения: 1) работа, выполняемая силой, равна изменению кинетической энергии системы, но 2) математически для консервативных сил выполненная работа равна минус изменению функции U , называемой потенциальной энергией. Как следствие этих утверждений возникает еще одно: если действуют только консервативные силы, сумма потенциальной U и кинетической Т энергий остается постоянной :
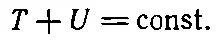 (14.2)
(14.2)
Рассмотрим формулу потенциальной энергии для ряда случаев. Если поле тяготения однородно, если мы не поднимаемся до высот, сравнимых с радиусом Земли, то сила постоянна и направлена вертикально, а работа равна просто произведению силы на расстояние по вертикали. Стало быть,
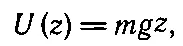 (14.3)
(14.3)
и за точку Р с нулевой потенциальной энергией можно принять любую точку на поверхности z=0. Но можно также говорить, что потенциальная энергия равна mg ( z -6), если нам так уж этого хочется! Все результаты в нашем анализе останутся теми же, кроме того что потенциальная энергия на поверхности z=0 будет равна - mg 6. Разницы никакой, ведь в расчет надо принимать только разности потенциальных энергий.
Энергия, необходимая для сжатия пружины на расстояние х от точки равновесия, равна
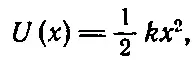 (14.4)
(14.4)
и нуль потенциальной энергии приходится на точку х =0, т. е. на равновесное состояние пружины. И здесь тоже мы можем добавить любую константу.
Потенциальная энергия тяготения точечных масс M и m на расстоянии r друг от друга равна
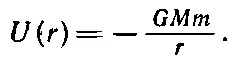 (14.5)
(14.5)
Константа здесь выбрана так, чтобы потенциал исчезал на бесконечности. Конечно, эту же формулу можно применить и к электрическим зарядам, поскольку закон один и тот же:
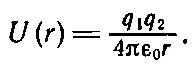 (14.6)
(14.6)
Давайте теперь поработаем с одной из этих формул, посмотрим, поняли ли мы их смысл.
Вопрос : С какой скоростью должна отправиться ракета с Земли, чтобы покинуть ее?
Ответ : Сумма кинетической и потенциальной энергий должна быть постоянной; покинуть Землю — значит удалиться от нее на миллионы километров; если у ракеты только-только хватает сил, чтобы покинуть Землю, то надо предположить, что там, вдалеке, ее скорость будет равна нулю и что на бесконечности она будет едва-едва двигаться. Пусть а — радиус Земли, а M — ее масса. Кинетическая плюс потенциальная энергии первоначально были равны 1/ 2 mv 2- GmM / a . В конце движения эти обе энергии должны сравняться. Кинетическую энергию в конце движения мы считаем нулевой, потому что тело еле движется (почти с нулевой скоростью), а потенциальная энергия равна величине GmM , деленной на бесконечность, т. е. опять нулевая. Значит, с одной стороны стоит разность двух нулей; поэтому квадрат скорости должен быть равен 2 GM / a . Но GM/a 2это как раз то, что называют ускорением силы тяжести g . Итак,
Читать дальше

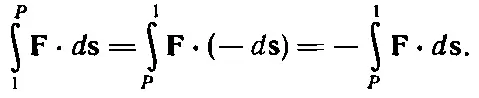
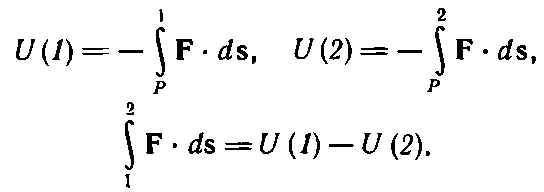 (14.1)
(14.1)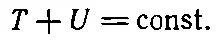 (14.2)
(14.2)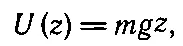 (14.3)
(14.3)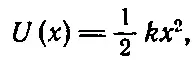 (14.4)
(14.4)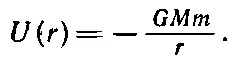 (14.5)
(14.5)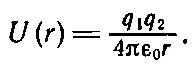 (14.6)
(14.6)




