Лоуренс Краусс - Почему мы существуем? Величайшая из когда-либо рассказанных историй

В действительности принцип неопределенности Гейзенберга как таковой не имеет вообще никакого отношения к наблюдателям, хотя и ограничивает – это правда – их способность проводить измерения. На самом же деле этот принцип представляет собой фундаментальное свойство квантовых систем, и его можно вывести относительно прямолинейно и математически, отталкиваясь от их волновых свойств.

Рассмотрим, к примеру, простое волноподобное возмущение с единственной частотой (и длиной волны), которое распространяется, колеблясь, вдоль направления x .

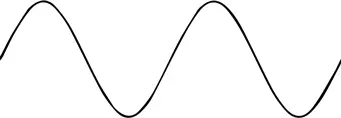
Как я уже отмечал, в квантовой механике частицы имеют волноподобный характер. Благодаря Максу Борну мы знаем, что для любой точки квадрат амплитуды, связанной с частицей волны – той, что мы сегодня вслед за Шрёдингером называем волновой функцией частицы, – определяет вероятность нахождения частицы в данной точке. Поскольку амплитуда изображенной на рисунке колеблющейся волны более или менее постоянна во всех пиках, такая волна, если она соответствует амплитуде вероятности обнаружения электрона, подразумевала бы более или менее равномерную вероятность его появления в любой точке вдоль траектории.

А теперь рассмотрим, как выглядело бы возмущение, если бы представляло собой сумму двух движущихся вдоль оси x волн с немного разными частотами (длинами):

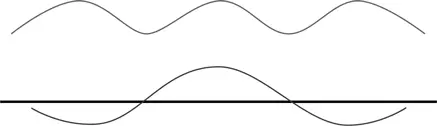
Складывая две волны, получим в результате следующее возмущение:

Из-за небольшого различия в длинах этих двух волн их пики и впадины будут в основном гасить друг друга, или «отрицательно интерферировать» всюду, за исключением редких участков, где совпадут два пика (одно из таких мест показано на рисунке). Это напоминает нам феномен волновой интерференции в эксперименте Юнга с двумя щелями, который я описывал выше.

Если мы добавим к этой комбинации еще одну волну с немного другой длиной,

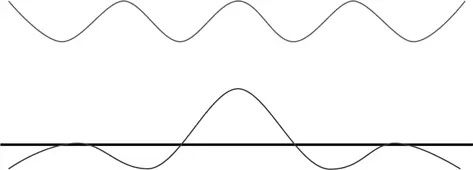
то результирующая волна будет выглядеть так:

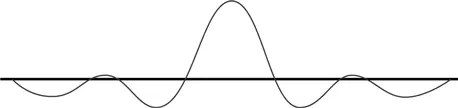
Интерференция размывает колебания еще сильнее, за исключением тех мест, где пики двух волн складываются, делая суммарную пиковую амплитуду волны намного выше, чем во всех остальных местах.

Можете сами представить, что произойдет, если я буду продолжать этот процесс, добавляя к первоначальной достаточно много других волн со слегка отличающимися частотами. Чем дальше, тем больше амплитуды волн будут гасить друг друга во всех точках, кроме некоторой небольшой области в центре рисунка и других отдаленных областей, где все пики могли бы вновь сойтись вместе.

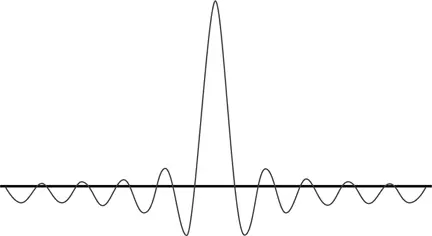
Чем больше число слегка различающихся частот, которые я складываю вместе, тем ýже окажется получившийся в итоге самый высокий центральный пик. А теперь представьте, что все это являет собой волновую функцию некой частицы. Чем больше амплитуда центрального пика, тем выше вероятность обнаружить частицу где-то в пределах ширины этого пика. Но ширина этого центрального пика все же никогда не становится совсем нулевой, так что возмущение остается распределенным по некоторой небольшой и все более сужающейся области.

Теперь вспомните: Планк и Эйнштейн рассказали нам, что, по крайней мере для световых волн, энергия каждого кванта излучения, то есть каждого фотона, прямо связана с его частотой. Неудивительно, что аналогичное соотношение действует и для волн вероятности, связанных с массивными частицами, но в этом случае с частотой, отвечающей частице волны, оказывается связан импульс частицы.

Отсюда и соотношение неопределенностей Гейзенберга: если мы хотим локализовать частицу в небольшой области, то есть получить как можно более узкий высочайший пик на ее волновой функции, то должны считать, что волновая функция получается сложением множества различных волн с чуть различающимися частотами. Но это означает, что импульс частицы, связанный с частотой ее волновой функции, должен быть несколько «размазан». Чем ýже доминантный пик волновой функции частицы, тем выше число различных частот (то есть импульсов), которые необходимо сложить, чтобы получить итоговую волновую функцию. Выражаясь более привычным языком, чем точнее мы хотим определить конкретное положение частицы, тем выше окажется неопределенность ее импульса.