Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]

Сейчас полагают, что расстояние до некоторых из них приблизительно равно половине размера Вселенной (10 26 м ) – наибольшего расстояния, которое можно себе представить!

Обратимся теперь к малым расстояниям. Подразделить метр просто. Без особых трудностей можно разделить его на тысячу равных частей. Таким же путем, хотя и несколько сложнее (используя хороший микроскоп), можно разделить миллиметр на тысячу частей и получить микрон (миллионную долю метра). Однако продолжать это деление становится трудно, поскольку невозможно «увидеть» объекты, меньшие, чем длина волны видимого света (около 5 ∙10 −7 м ).

Все же мы не останавливаемся на том, что недоступно глазу. С помощью электронного микроскопа можно получить фотографии, помогающие увидеть и измерить еще меньшие объекты – вплоть до 10 −8 м (фиг. 5.9).

Фиг. 5.9. Фотография вирусов, полученная с помощью электронного микроскопа. Видна «большая» сфера, показанная для сравнения: диаметр ее равен 2 ∙10 −7м, или 2000 Å.

А с помощью косвенных измерений (своего рода триангуляции в микроскопическом масштабе) можно измерять всё меньшие и меньшие объекты. Сначала из наблюдений отражения света короткой длины волны (рентгеновских лучей) от образца с нанесенными на известном расстоянии метками измеряется длина волны световых колебаний.

Затем по картине рассеяния того же света на кристалле можно определить относительное расположение в нем атомов, причем результат хорошо согласуется с данными о расположении атомов, полученными химическим путем. Таким способом определяется диаметр атомов (около 10 −10 м ).

Дальше в шкале расстояний имеется довольно большая незаполненная «щель» между атомными размерами 10 −10 м и в 10 5раз меньшими ядерными размерами (около 10 −15 м ). Для определения ядерных размеров применяются уже совершенно другие методы: измеряется видимая площадь σ, или так называемое эффективное поперечное сечение . Если же мы хотим определить радиус, то пользуемся формулой σ = πr 2, поскольку ядра можно приближенно рассматривать как сферические.

Эффективные сечения ядер можно определить, пропуская пучок частиц высокой энергии через тонкую пластинку вещества и измеряя число частиц, не прошедших сквозь нее. Эти высокоэнергетические частицы прорываются сквозь легкое облачко электронов, но при попадании в тяжелое ядро останавливаются или отклоняются. Предположим, что у нас имеется пластинка толщиной 1 см . На такой толщине укладывается приблизительно 10 8атомных слоев. Однако ядра настолько малы, что вероятность того, что одно ядро закроет другое, очень незначительна. Можно себе представить, что высокоэнергетическая частица, налетающая на пластинку углерода толщиной 1 см , «видит» приблизительно то, что в сильно увеличенном масштабе показано на фиг. 5.10.

Фиг. 5.10. Воображаемая пластинка углерода толщиной 1 см при сильном увеличении (если бы были видны только ядра атомов).

Вероятность того, что очень малая частица столкнется с ядром, равна отношению площади, занимаемой ядрами (черные точки), к общей площади рисунка. Пусть над областью с площадью А по всей толщине пластинки находится N атомов (разумеется, каждый с одним ядром). Тогда доля площади, закрытая ядрами, будет равна Nσ/A . Пусть теперь число частиц в нашем пучке до пластинки будет равно n 1, а после нее равно n 2; тогда доля частиц, не прошедших через пластинку, будет ( n 1− n 2)/ n 1,что должно быть равно доле площади, занимаемой ядрами. Радиус же ядер вычисляется из равенства [5] Это равенство справедливо только тогда, когда площадь, занимаемая ядрами, составляет малую долю общей площади, т. е. ( n 1- n 2)/ n 1 много меньше единицы. В противном же случае необходимо учитывать поправку на частичное «загораживание» одного ядра другим.

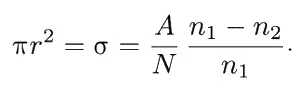
Из таких экспериментов мы находим, что радиусы ядер лежат в пределах от 1 ∙10 −15до 6 ∙10 −15 м . Кстати, единица длины 10 −15 м называется ферми в честь Энрико Ферми (1901–1958).