Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]

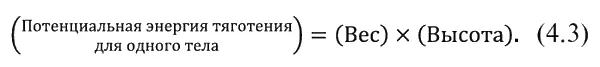
Не правда ли, очень красивое рассуждение? Вопрос только в том, справедливо ли оно. (Ведь, в конце концов, природа не обязана следовать нашим рассуждениям.) Например, не исключено, что в действительности вечное движение возможно. Или другие предположения ошибочны. Или мы просмотрели что-то в своих рассуждениях. Поэтому их непременно нужно проверить. И вот – справедливость их подтверждает опыт.

Потенциальная энергия – это общее название для энергии, связанной с расположением по отношению к чему-либо. В данном частном случае это – потенциальная энергия тяготения . Если же производится работа против электрических сил, а не сил тяготения, если мы «поднимаем» заряды «над» другими зарядами с помощью многочисленных рычагов, тогда запас энергии именуется электрической потенциальной энергией . Общий принцип состоит в том, что изменения энергии равны силе, умноженной на то расстояние, на котором она действует:

По мере чтения курса мы еще не раз будем возвращаться к другим видам потенциальной энергии.

Принцип сохранения энергии во многих обстоятельствах оказывается очень полезен при предсказании того, что может произойти. В средней школе мы учили немало правил о блоках и рычагах. Мы можем теперь убедиться, что все эти «законы» сводятся к одному , и нет нужды запоминать 75 правил. Вот вам простой пример: наклонная плоскость. Пусть это треугольник со сторонами 3, 4, 5 (фиг. 4.3).

Подвесим к блочку груз весом 1 кг и положим его на плоскость, а с другой стороны подвесим груз W.

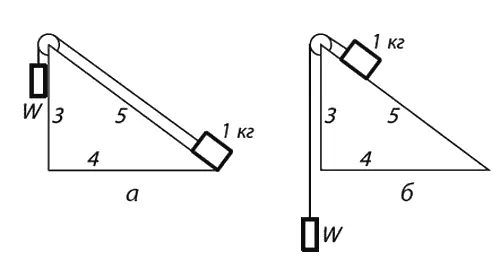
Фиг. 4.3. Наклонная плоскость.

Мы хотим знать, какова должна быть тяжесть W , чтобы уравновесить груз 1 кг . Рассуждаем так. Если грузы W и 1 кг уравновешены, то это – обратимое состояние, и веревку можно двигать вверх-вниз. Пусть же вначале (фиг. 4.3, а ) 1 кг находится внизу плоскости, а груз W – наверху. Когда W соскользнет вниз, груз 1 кг окажется наверху, a W опустится на длину склона (фиг. 4.3, б ), т. е. на 5 м . Но ведь мы подняли 1 кг только на высоту 3 м , хотя опустили W на 5 м . Значит, W = 3/ 5 кг . Заметьте, что этот ловкий вывод получен не из разложения сил, а из сохранения энергии . Ловкость, впрочем, относительна. Существует другой вывод, куда красивее. Он придуман Стевином и даже высечен на его надгробии. Фиг. 4.4 объясняет, почему должно получиться 3/ 5 кг : цепь не вращается и нижняя ее часть уравновешена сама собой, значит сила тяги пяти звеньев с одной стороны должна уравнять силу тяги трех звеньев с другой (по длине сторон).

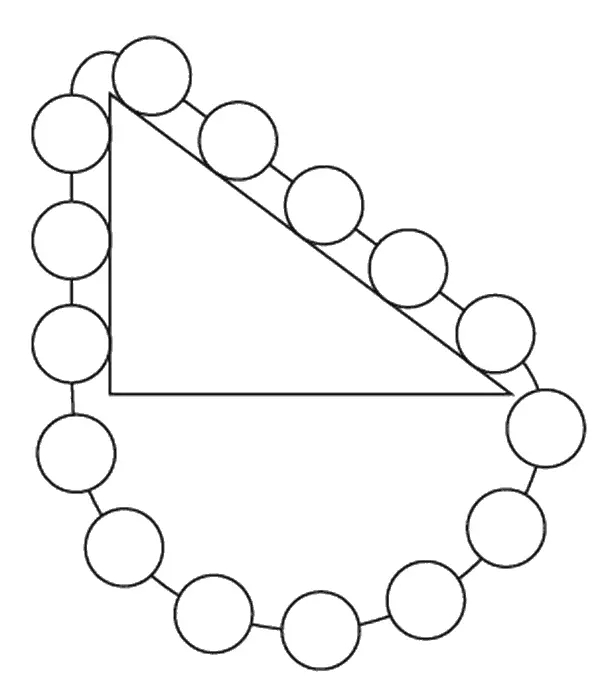
Фиг. 4.4. Это выгравировано на надгробии Стевина.

Глядя на диаграмму, становится очевидно, что W = 3/ 5 кг. (Неплохо было бы, если бы когда-нибудь что-нибудь подобное высекли и на вашем надгробном камне.)

А вот задача посложнее: домкрат, показанный на фиг. 4.5.

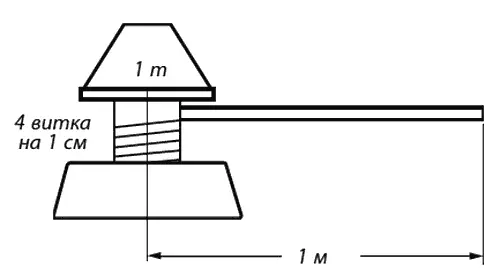
Фиг. 4.5. Домкрат.

Посмотрим, как в таком случае применять этот принцип. Для вращения домкрата служит ручка длиной 1 м , а нарезка винта имеет 4 витка на 1 см . Какую силу нужно приложить к ручке, чтобы поднять 1 m ? Желая поднять 1 т на 1 см , мы должны обойти домкрат четырежды, каждый раз делая по 6,28 м (2 πr ), а всего 25,12 м . Используя различные блоки и т. п., мы действительно можем поднять 1 т с помощью неизвестного груза W , приложенного к концу ручки. Ясно, что W равно примерно 400 г . Это – следствие сохранения энергии.

И еще более сложный пример (фиг. 4.6).

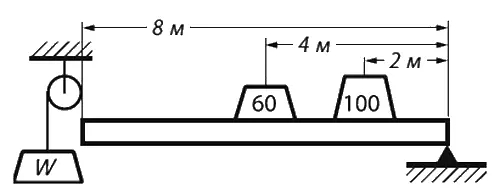
Фиг. 4.6. Нагруженный стержень, подпертый с одного конца.

Подопрем один конец стержня (или рейки) длиной 8 м . Посредине рейки поместим груз весом 60 кг , а в 2 м от подпорки – груз весом 100 кг . Сколько надо силы, чтобы удержать рейку за другой конец в равновесии, пренебрегая ее весом? Пусть мы прикрепили блок и перекинули через него веревку, привязав ее к концу рейки. Каков же должен быть вес W , уравновешивающий стержень? Представим, что вес опустился на произвольное расстояние (для простоты пусть это будет 4 см );на сколько тогда поднимутся наши два груза? Середина рейки на 2 см , а второй груз (он лежит на четверти длины рейки) на 1 см . Значит, в согласии с правилом, что сумма весов, умноженных на высоты, не меняется, мы должны написать: вес W на 4 см вниз плюс 60 кг на 2 см вверх плюс 100 кг на 1 см вверх, что после сложения должно дать нуль: