Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]

Представим, что имеются два класса машин – необратимые (сюда входят все реальные машины) и обратимые , которых на самом деле не существует; как бы тщательно ни изготавливать подшипники, рычаги и т. д., таких машин все равно не построишь. Но мы предположим все же, что обратимая машина существует и способна, опустив единичный груз (килограмм или грамм – все равно) на единичную длину, поднять в то же время тройной груз. Назовем эту обратимую машину машиной А. Положим, что данная обратимая машина подымает тройной груз на высоту X. Затем предположим, что имеется другая машина В , не обязательно обратимая, которая тоже опускает единичный вес на единицу длины, но поднимает тройной вес на высоту Y. Теперь можно доказать, что Y не больше X , т. е. что нельзя соорудить машину, которая смогла бы поднять груз выше , чем обратимая. Почему? Посмотрите. Пусть Y выше X . Мы берем единичный вес и опускаем его на единицу длины машиной В , тем самым поднимая тройной груз на высоту Y . Затем мы можем опустить груз с высоты Y до X, получив свободную энергию , и включить обратимую машину А в обратную сторону, чтобы опустить тройной груз на X и поднять единичный вес на единичную высоту. Единичный вес очутится там, где он был прежде, и обе машины окажутся в состоянии начать работу сызнова! Итак, если Y больше X , то возникает вечный двигатель, а мы предположили, что такого не бывает. Мы приходим к выводу, что Y не выше X , т. е. из всех машин, которые можно соорудить, обратимая – наилучшая.

Легко понять также, что все обратимые машины должны поднимать груз на одну и ту же высоту . Положим, что машина В также обратима. То, что Y не больше X , остается, конечно, верным, но мы можем пустить машину в обратную сторону, повторить те же рассуждения и получить, что X не больше Y. Это очень знаменательное наблюдение, ибо оно позволяет узнать, на какую высоту разные машины могут поднимать грузы, не заглядывая в их внутреннее устройство . Если кто-нибудь придумал невероятно запутанную систему рычагов для подъема тройного веса на какую-то высоту за счет опускания единичного веса на единицу высоты и если мы сравним эту машину с простым обратимым рычагом, способным проделать то же самое, то первая машина не поднимет вес выше второй (скорее, наоборот). А если его машина обратима, то мы знаем точно, на какую высоту она будет поднимать грузы.

Вывод : каждая обратимая машина, как бы она ни действовала, опуская 1 кг на 1 м , всегда подымает 3 кг на одну и ту же высоту X. Ясно, что мы доказали очень полезный всеобщий закон. Но возникает вопрос: чему равно X ?

Пусть у нас есть обратимая машина, способная поднимать 3 кг за счет 1 кг на высоту X. Поместим три шара на стеллаж (как на фиг. 4.2).

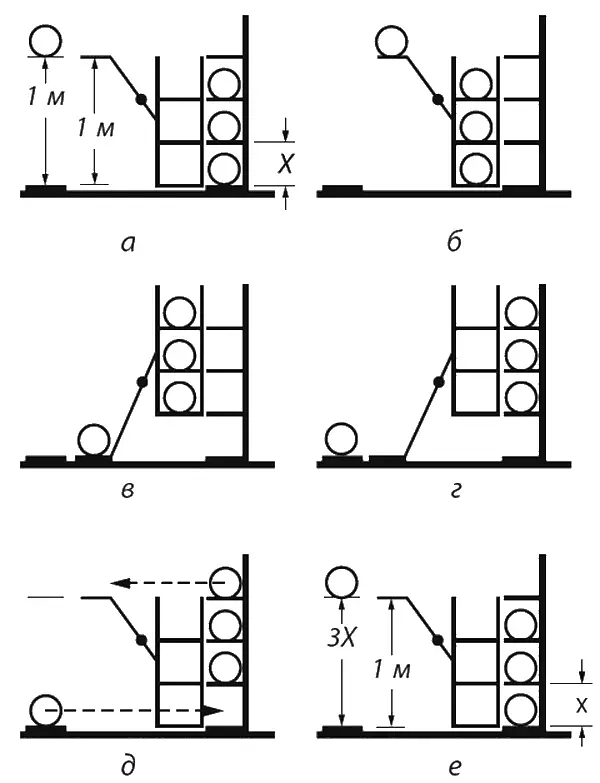
Фиг. 4.2. Обратимая машина.

а – начальное положение; б – загрузка шаров; в – 1 кг поднимает 3 кг на высоту X; г – разгрузка шаров; д – восстановление; е – конечное положение.

Четвертый лежит на подставке в одном метре от пола. Машина может поднять три шара, опустив один шар на 1 м . Устроим подвижную платформу с тремя полками высотой X , и пусть высота полок стеллажа тоже будет X (фиг. 4.2, а ). Перекатим сперва шары со стеллажа на полки платформы (фиг. 4.2, б ); предположим, что для этого энергии не понадобится, потому что полки и стеллаж находятся на одной высоте. Затем включим обратимую машину: она скатит одиночный шар на пол и подымет платформу на высоту X (фиг. 4.2, в ). Но мы сконструировали платформу столь остроумно, что шары опять оказались в точности на уровне полок стеллажа. Разгрузим же шары с платформы на стеллаж (фиг. 4.2, г ). После разгрузки машина вернется в первоначальное положение. Теперь уже три шара лежат на трех верхних полках стеллажа, а четвертый шар – на полу. Но смотрите, какая странная вещь: по существу два шара мы не поднимали вовсе, ведь на полках 2 и 3 шары как лежали вначале, так лежат и теперь. В итоге поднялся только один шар , но зато на высоту 3 Х . Если бы высота 3 Х оказалась больше 1 м , то можно было бы опустить шар, чтобы вернуть машину к начальным условиям (фиг. 4.2, е ) и начать работу сначала. Значит, высота 3 Х не может быть больше 1 м , ибо начнется вечное движение. Точно так же можно доказать, что 1 м не может быть больше 3 Х : машина обратима, пустим ее назад и докажем. Итак, 3 Х ни больше ни меньше 1 м . Мы открыли при помощи одних только рассуждений закон: Х = 1/ 3 м . Обобщить его легко; 1 кг падает при работе обратимой машины с некоторой высоты; тогда машина способна поднять р кг на 1/ р высоты. Если, другими словами, 3 кг умножить на высоту их подъема ( X ), то это равно 1 кг , умноженному на высоту его падения (1 м ). Помножив все грузы в машине на высоту, на которой они лежат, дайте машине поработать и опять помножьте все веса на их высоты подъема; в итоге должно выйти то же самое. (Мы перешли от случая, когда двигался только один груз, к случаю, когда за счет опускания одного груза поднимается несколько грузов. Но это, надеюсь, понятно?) Назовем сумму весов, умноженных на высоту, потенциальной энергией тяготения , т. е. энергией, которой обладает тело вследствие своего положения в пространстве по отношению к земле. Формула для энергии тяготения, пока тело не слишком далеко от земли (вес при подъеме ослабляется), такова: