Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Оценка времени схлопывания пузырька

Давайте оценим продолжительность времени схлопывания пузырька. Как и прежде, применим к массе воды m , которая устремляется внутрь пузырька во время схлопывания, второй закон Ньютона:

ma r = F p,

где F p – сила, возникающая из-за разности давлений, а a r – ускорение границы пузырька. Для силы давления можно записать: F p = S Δ P , где S = 4π R 2 – площадь поверхности пузырька и Δ P – разница давлений на границе пузырька. Оценивая массу m как (4/3) πρ R 3(объем пузырька, умноженный на плотность воды), получаем ρ R 3 a r /3 = R 2Δ P . Примем разность давлений Δ P (которое зависит только от разности температур между нижним и верхним слоями воды) за константу. Если t 2 – время, за которое пузырек схлопывается, и R 0 – изначальный радиус пузыря, то ускорение a r можно принять за R 0 / t 2 2и прийти к оценке:

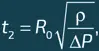
где мы опустили под корнем коэффициент 3, который, учитывая приблизительный характер вычислений, не сильно влияет на результат. При нормальных условиях давление насыщенного пара уменьшается примерно на 3 кПа на градус (см. таблицу в главе 15). Поэтому примем Δ P равным 1 кПа. В таком случае пузырек радиуса 1 мм схлопнется примерно за 1 мс.

Во время самого кипения тональность снова меняется: теперь шум возникает из-за разрыва пузырьков на поверхности. Спектр испускаемого звука зависит также от формы чайника и уровня воды в нем. Пение кипящей воды изучал еще в XVIII веке шотландский физик Джозеф Блэк (1728–1799). Он пришел к заключению, что возникающий звук – это результат дуэта поднимающихся к поверхности пузырьков и вибраций стенок чайника.

Но вот в одном из чайников температура поднялась достаточно, чтобы пузырьки пара достигли поверхности и лопнули на ней (илл. 4). Как и следовало ожидать, в накрытом крышкой чайнике вода нагрелась быстрее – об этом свидетельствует вырывающийся из носика пар. Сам по себе водяной пар невидим, но на выходе из носика он частично конденсируется в капельки воды. Именно эти сопровождающие поток капельки, благодаря рассеянию света Ми, которое мы уже обсудили выше (см. главу 3, «Цвет облаков»), делают его похожим на белое облако. Струя пара оказывается достаточно сильной, чтобы заставить звучать свисток (см. врезку). Кроме того, она может обжечь руку, случайно оказавшуюся на ее пути. Убрав ее всего лишь через полсекунды, мы получим порцию водяного пара массой порядка 0,1 г. Это подводит к новому вопросу…

4. Поднимающиеся в процессе кипения пузырьки пара растут в размерах. Начиная с определенного радиуса, они уже не сохраняют сферическую форму. Пузырьки поднимаются на поверхность, которая бурлит, словно море во время жестокого шторма

Что обжигает сильнее: кипяток или водяной пар? Это вопрос из разряда: «Что тяжелее: железо или вата?» Или другой его распространенный вариант: «Что тяжелее: 1 килограмм ваты или 1 килограмм железа?» Так и нам следует уточнить: «Что обжигает сильнее: грамм кипящей воды или грамм стоградусного водяного пара?» Не будем тянуть с ответом: конечно же, водяной пар! На более холодной поверхности, такой как кожа, он начинает конденсироваться, а затем охлаждается. В процессе конденсации массы m водяного пара при 100 °C выделяется скрытая теплота парообразования mr , которая была ранее затрачена на то, чтобы этот пар перевести из жидкого состояния в парообразное. Величина r называется удельной теплотой парообразования, и для воды она составляет 2257 кДж⋅кг –1(см. главу 18, «Откуда идет тепло?»). Эта энергия оказывается намного больше чем та, что выделится при дальнейшем охлаждении той же массы воды. Действительно, последняя равна mC Δ T , где C = 4190 Дж⋅кг –1°C –1 – удельная теплоемкость воды, а Δ T – разница между конечной (около 40 °C, когда контакт с кожей становится терпимым) и начальной (100 °C) температурами. Легко убедиться, что при Δ T = 60 °C соотношение между выделенными энергиями составляет примерно 10 раз. Таким образом, вода в парообразном состоянии обжигает в десять раз сильнее, чем в жидком.