Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Почему при нагревании воды образуются пузырьки, каким газом они наполнены? Поначалу это пузырьки растворенного в воде воздуха (см. главу 14, «Пузырьки шампанского»). По мере того как температура воды возрастает, пузырьки все больше и больше заполняются водяным паром. Для того чтобы пузырек радиуса R был «жизнеспособен», давление внутри него должно превышать внешнее давление на величину δ P = 2σ/ R , где σ – коэффициент поверхностного натяжения воды. Эта дополнительная величина называется давлением Лапласа (см. главу 6, «Формула Лапласа»). В нашем случае внешнее давление – это давление жидкости, то есть оно практически равно атмосферному (давление столба жидкости в чайнике пренебрежимо мало по сравнению с атмосферным). Что же касается давления внутри пузырька, то оно определяется суммой давлений содержащегося в нем воздуха и насыщенного пара. Последнее – это давление пара, находящегося в равновесии со своей жидкостью при заданной температуре. С ростом температуры давление насыщенного пара очень быстро возрастает (см. таблицу). Поэтому пузырьки в первую очередь появляются именно на более горячем дне чайника. Но даже там зарождение пузырька происходит непросто: ведь вначале, пока радиус пузырька еще мал, давление Лапласа, которому следует противостоять воздуху и пару, очень велико! Опыты показали, что возникновение пузырьков чаще всего происходит на дефектах дна чайника, где условия для зарождения более благоприятны: начальный размер пузырька определяется характерным размером дефекта (илл. 2). При этом говорят, что подобное зарождение гетерогенно , в отличие от гомогенного зарождения – в случае, если пузырьки появляются в объеме жидкости.

Рассмотрим подробно уравнения, которые описывают движение пузырька при его восхождении. Будем считать пузырек сферой постоянного радиуса, что не совсем верно, однако приведет нас к достаточно точному результату. Итак, на пузырек действуют его вес (незначительный), сила Архимеда и сила сопротивления его движению.

Для сферического пузырька радиуса R сила Архимеда F а равна:

F А = (4/3) πρ gR 3,

где ρ и g – плотность воды и ускорение свободного падения соответственно.

Сила сопротивления F с движению тела сферической формы в вязкой среде с небольшой скоростью определяется формулой Стокса:

F С = –6πη Rv ,

где η – коэффициент вязкости воды и v – скорость пузырька.

При более высоких скоростях уже играет роль не вязкость, а сила лобового сопротивления движению сферы, и ее можно найти по формуле:

F лс ≈ –πρ R 2 v 2/2.

Эти два выражения для силы сопротивления удобно связать между собой посредством так называемого числа Рейнольдса (безразмерной величины, очень полезной в механике жидкостей) Re = ρ Rv /η:

F лс = (Re/12) F С.

Для сферы диаметром 1 мм в воде число Re составляет порядка 200. Поэтому для оценки силы сопротивления мы используем формулу для силы лобового сопротивления, которая дает в достаточной мере точный результат.

Таким образом, действующая на пузырек результирующая сила F = F А + F лс . Второй закон Ньютона (см. главу 4, «Ньютоновская механика») позволяет получить уравнение движения объекта при условии, что известна его масса m : векторная сумма внешних сил, воздействующих на объект, равна его ускорению, умноженному на массу, то есть

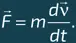
В рассматриваемом случае, когда движущимся в жидкости объектом является пузырек пренебрежимо малой массы, найденная результирующая сила главным образом придает ускорение жидкости, вовлекаемой в движение на пути пузырька вверх. Как же написать для нее второй закон Ньютона? Какую массу и ускорение чего в него подставлять? Задача представляется неразрешимой! К счастью, из механики жидкостей известно, что второй закон Ньютона применим и к погруженному в жидкость сферическому объекту при условии добавления к его собственной массе некоторой дополнительной, так называемой присоединенной массы δ m = (2/3) πρ R 3. Эта величина учитывает необходимость вовлечения в движение окружающих сферический объект слоев жидкости и, как это ни странно, оказывается равной половине массы жидкости, которая потребовалась бы, чтобы эту сферу заполнить. Для движущегося в воде пузырька полная масса m практически равна присоединенной массе δ m . В первые мгновения после отрыва пузырька ото дна его скорость еще мала, сопротивление воды незначительно и второй закон Ньютона приобретает вид: F А = δ m d v/ d t, что после подстановки выражений для силы Архимеда и присоединенной массы приводит к удивительному результату: dv/dt = 2 g . Следовательно, ускорение пузырька на начальном этапе его движения в два раза превышает ускорение свободного падения и направлено, конечно же, вверх, а не вниз.