Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Но вернемся к теме этой главы – ядерному магнитному моменту. Представление о простейшем атоме можно получить на примере точечного электрического заряда q , описывающего под действием электростатического притяжения окружность вокруг неподвижного заряда противоположного знака (илл. а).

Пусть на этот заряд также воздействует магнитное поле B →(илл. b). Теперь, кроме электростатической силы притяжения к неподвижному центру, на движущийся заряд воздействует еще и сила Лоренца, направленная перпендикулярно полю и вектору скорости v →и равная по модулю B νsinα, где α – угол между B →и v →. В терминах векторного произведения (см. главу 4, врезку «Смысл силы Кориолиса и векторное произведение») силу Лоренца можно записать как F →= qv →× B →. Это выражение напоминает о силе Кориолиса, появляющейся при написании уравнений движения для тела в системе отсчета, которая сама вращается вокруг оси с угловой скоростью Ω. Как мы уже знаем, в этом случае в баланс воздействующих на тело сил необходимо добавить фиктивную силу, равную mv →× Ω →, где Ω → – вектор угловой скорости, параллельный оси вращения (см. главу 4). Выражения для двух сил, Кориолиса и Лоренца, очень схожи! Особенно если векторы Ω →и B →параллельны. В этом случае можно даже сделать такой трюк, чтобы обе силы скомпенсировали друг друга! Для этого достаточно выбрать Ω = – qB / m . Иначе говоря, надо перейти в систему координат, которая вращается вокруг вектора B →с угловой скоростью – qB / m . В этой системе отсчета магнитное поле и сила Лоренца сокращаются, и все происходит так, как будто заряд A испытывает лишь электростатическое притяжение. То есть его орбита во вращающейся системе отсчета оказывается неподвижной, в то время как в фиксированной системе координат она вращается с угловой скоростью qB / m . А вместе с ней вращается и магнитный момент. Вот вам и прецессия! Этот результат остается неизменным и в квантовой механике: магнитный момент спина в магнитном поле также подвержен прецессии.

Хотя в системе, которую мы только что изучили, имеет место прецессия, ей не подвержен намагниченный стержень (например, стрелка компаса)! Пребывая в магнитное поле, будучи отклоненным от своего положения равновесия и отпущенным без какой-либо начальной скорости, магнитный стержень колеблется без вращения вокруг поля. В конце концов его колебания из-за трения затухнут, и стержень принимает направление север – юг.

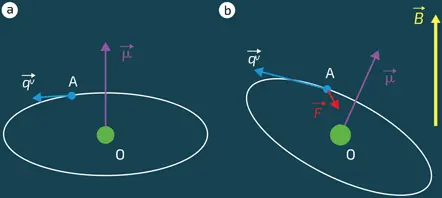
Ларморовская прецессия. а.Заряд q, вращаясь вокруг точки O, создает магнитный момент (фиолетовая стрелка). b.При воздействии на него внешнего поля B →возникает сила Лоренца (красная стрелка), которая посредством перехода во вращающуюся систему координат может быть скомпенсирована возникающей при этом силой Кориолиса. Таким образом, в этой системе магнитный момент (фиолетовая стрелка) оказывается неподвижным. Однако при этом относительно неподвижного наблюдателя он вращается. В этом и заключается явление прецессии

После открытия Блоха и Парселла ядерная магнитно-резонансная спектрометрия стала бурно развиваться. Во Франции и Италии появились крупные исследовательские группы по ЯМР. Французские физики Анатоль Абрагам и Ионель Соломон, итальянец Луиджи Джулотто основали всемирно известные научные школы в Париже и Павии. Подобные группы стали движущей силой запуска объединения Ampère (Ампер), которое способствовало научному прогрессу в этой области. ЯМР повсеместно применяется в физике твердых тел, химии, биологии, метрологии. И, конечно же, физики не стали тянуть с началом применения ЯМР в медицине. Первое двумерное изображение двух образцов с водой было получено в 1973 году американским химиком Полом Лотербуром. В 1976 году американский ученый Реймонд Дамадья представил первое ЯМР-изображение опухоли животного. Сегодня многие больницы оснащены аппаратами МРТ для медицинской диагностики (илл. 8).

Опишем принцип формирования изображения методом магнитно-резонансной томографии. Этот метод, использующий неоднородное в пространстве магнитное поле B →, был предложен Полом Лотербуром (илл. 9) в 1973 году. В результате зависящая от значения поля B (см. формулу (2)) резонансная частота ядра оказывается зависящей от положения ядра в пространстве.