Квантование потока в витке сверхпроводника
Найдем с помощью упрощенных рассуждений формулу, описывающую квантование потока в сверхпроводнике. Рассмотрим случай кругового кольца с нулевым сопротивлением, содержащего свободные заряженные частицы. С возрастанием магнитного поля растет и магнитный поток Φ, что приводит к возникновению электродвижущей силы индукции (см. главу 16, «Электромагнитная индукция»):
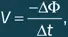
где ΔΦ – изменение потока, происходящее за время Δ t . При этом индуцируемое в кольце электрическое поле равно:
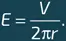
Теперь рассмотрим заряд q массы m , движущийся по кольцу со скоростью ν (илл. 1). Воздействующая на него сила равна q E , и, согласно основному принципу динамики (см. главу 4, врезку «Ньютоновская механика»), испытываемое зарядом ускорение равно q E /m. Это ускорение должно быть равно отношению увеличения скорости Δ v ко времени Δ t , следовательно:
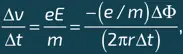
откуда находим, что 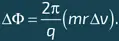
Предполагая, что правило квантования Бора mrv = nħ , упомянутое в начале этой главы, применимо к движению рассматриваемого заряда в сверхпроводящем кольце, находим, что наименьшее ненулевое значение m r Δ v равно ħ . Отсюда следует, что наименьшее ненулевое значение ΔΦ равно 2π ħ /q. Заряд куперовской пары равен 2e: таким образом, мы приходим к формуле квантования потока в сверхпроводнике, приведенной в тексте.
А что случится, если поместить кольцо в переменное магнитное поле B ? Для «нормального» проводника пронизывающий кольцо магнитный поток Φ изменяется вместе с полем. В результате возникает электродвижущая сила индукции d Φ /dt , которая порождает в кольце ток I N , такой, что RI N = d Φ/ dt , где R – сопротивление кольца. Для сверхпроводника, как мы уже знаем, поток должен оставаться неизменным, иначе его изменение вызвало бы бесконечный ток, разрушающий сверхпроводящее состояние. Поэтому по сверхпроводящему кольцу при изменении магнитного поля также будет течь ток I S , такой, чтобы пронизывающий кольцо полный поток Φ (являющийся суммой внешнего потока Φ внеш = BS и собственного индукционного потока Φ I = LI S , где L – индуктивность кольца) не изменялся.
Туннельный эффект и эффект Джозефсона
Ситуация становится еще интереснее, если сверхпроводящее кольцо прерывается тонким слоем диэлектрика. Предположим, что мы сумели создать такую тончайшую перемычку в кольце, изготовленном из нормального металла (илл. 2). Интуитивно кажется, что ток в нем течь не сможет. И тем не менее, если толщина диэлектрической перемычки не слишком велика (например, около микрометра), ток в такой структуре может протекать! Некоторым электронам «волшебным» образом удается пройти через диэлектрик. Это чисто квантовое явление называется «туннельным эффектом». Например, при изучении объектов с помощью туннельного микроскопа ток проходит между острием устройства и поверхностью образца через зазор вакуума, имеющий размер порядка нанометра (см. главу 28, «Взгляд в наномир»). Туннелировать с некоторой вероятностью сквозь «стены» в квантовом мире могут не только электроны, но и другие, более массивные частицы, даже такие, как атомные ядра. Правда, с увеличением массы совершать эти чудеса им становится все сложнее и сложнее.
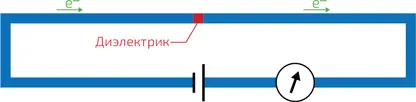
2. Туннельный эффект в проводящем кольце, содержащем диэлектрический барьер (отмечен красным цветом). Если прослойка диэлектрика не слишком велика, то электроны благодаря туннельному эффекту с некоторой вероятностью проходят через него. Протекающий в кольце ток измеряется амперметром
А что же произойдет в случае сверхпроводящего кольца? Оказывается, что и здесь имеет место своеобразный туннельный эффект. Куперовским парам удается преодолевать слой диэлектрика толщиной в несколько нанометров или слой нормального металла толщиной в десяток нанометров. Казалось бы, что для таких составных бозонов механизм туннелирования должен заключаться в последовательном проникновении через стенку сперва одного, а затем другого электрона, то есть соответствующий сверхпроводящий ток должен быть пропорциональным квадрату и так малой вероятности проникновения электрона сквозь барьер. Однако еще одной диковиной сверхпроводимости оказывается тот факт, что, будучи, как мы уже знаем, довольно размазанными в пространстве объектами, куперовские пары туннелируют сквозь барьер примерно с той же вероятностью, что и каждый электрон, их составляющий. Можно сказать, что оба электрона каким-то образом туннелируют когерентно, одновременно. Это явление было предсказано в 1962 году англичанином Брайаном Джозефсоном (в то время всего лишь 22-летним аспирантом Кембриджского университета), а придуманный им «сэндвич» – диэлектрический слой между двумя сверхпроводниками – называется «джозефсоновским контактом».
Читать дальше
Конец ознакомительного отрывка
Купить книгу

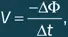
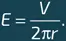
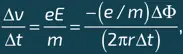
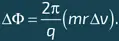




![Лина Сайфер - Театр мыльных пузырей [litres]](/books/434478/lina-sajfer-teatr-mylnyh-puzyrej-litres-thumb.webp)






