Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Во втором случае рассмотрим сверхпроводник в мейснеровском состоянии, то есть помещенный в магнитное поле ниже первого критического. Здесь возбужденный в сверхпроводнике постоянный ток действительно окажется вечным. Неужели это и есть то вечное движение, о котором мечтали ученые прошлых веков? В некотором смысле да, ведь с током в классической физике связано движение заряженных частиц. Однако в квантовой механике это явление имеет смысл, существенно отличающийся от своего классического толкования. В классической механике наблюдаемые величины хорошо определены – например, положение частиц, которое зависят от времени. Поэтому при наличии тока здесь можно уверенно говорить о перемещении зарядов в пространстве. Сверхпроводящий же ток в условиях приложенного магнитного поля – это реакция всего конденсата на внешнее воздействие, которая спасает сверхпроводящее состояние от разрушения. Сверхпроводник в таком токовом состоянии находится в термодинамическом равновесии и может пребывать в нем бесконечно долго.

Таким образом, сверхпроводимость – это редкий случай проявления законов квантовой механики в окружающем нас макроскопическом мире.

В предыдущей главе мы в общих чертах рассказали о явлении сверхпроводимости как таковом и о долгом пути ученых к пониманию его квантовой природы. В этой главе мы продолжим наш рассказ о необычных свойствах сверхпроводников и остановимся на способах их применения, которые мало знакомы широкой публике.

Как мы уже видели, Нильсу Бору удалось объяснить многие свойства атома, предположив, что скорость v электрона на круговой орбите радиуса R удовлетворяет отношению m ν R = nħ , где n – целое число, m – масса электрона и ħ – постоянная Планка (см. главу 22). Замечательно, что это правило может быть обобщено для описания движения любой частицы, совершающей круговое движение в определенном квантовом состоянии. Отметим, что как раз к движению электрона в атоме постулат Бора применим не очень хорошо, поскольку электрон четко определенную орбиту не описывает (иначе нарушались бы соотношения неопределенности (см. главу 22, «Спектр излучения атомов – ключ к атомной структуре»)). С другой стороны, как показал Фриц Лондон (1900–1954) в 1948 году, он может быть успешно применен к сверхпроводящему току, текущему в круговом кольце радиуса R (илл. 1).

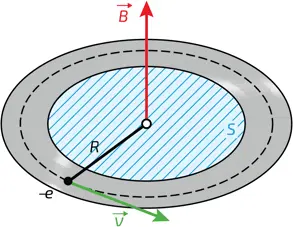
1. Ток в кольце радиуса R. Поток магнитной индукции через кольцо Φ = BS , где S – охватываемая кольцом площадь, а B – магнитное поле. Применяя к движущемуся заряду правило квантования Бора, находят, что этот поток квантуется

Правило квантования Бора, примененное к движению куперовских пар в сверхпроводящем кольце (см. главу 24, «Теория БКШ»), имеет неожиданное следствие: магнитный поток через сверхпроводящее кольцо квантуется – так же как и радиус орбиты в атоме! Точнее, магнитный поток Φ оказывается целым кратным «кванта магнитного потока»:

Φ 0 = π ħ /e = h/(2e) = 2∙10 –15Тл∙м 2,

где – е – заряд электрона (см. врезку «Квантование потока в витке сверхпроводника»).

Квант потока Φ 0 – чрезвычайно малая величина, настолько малая, что первую экспериментальную проверку гипотезы Лондона американским физикам Бэскому Диверу и Уильяму Фэйрбэнку удалось провести только 13 лет спустя, в 1961 году.

Примечательно, что в то время, как квантованные физические величины, упоминаемые нами до сих пор, принадлежали к микроскопическому миру, квант магнитного потока ученым удается измерить в относительно больших, почти макроскопических образцах (то есть видимых невооруженным глазом). Примером таких «мезоскопических», то есть промежуточных между микро- и макромирами объектов, являются вихри Абрикосова, которые могут находиться друг от друга на расстояниях в микрометры. Напомним, что эти вихри возникают в сверхпроводнике II рода, помещенном во внешнее магнитное поле (см. главу 24, «Вихри Абрикосова»). Каждый абрикосовский вихрь является носителем кванта магнитного потока Φ 0 . Еще одним подобным примером являются сверхпроводящие кольца, которые позволяют наблюдать дискретное изменение пронизывающего их магнитного потока буквально по одному кванту Φ 0 (см. ниже). Подобные наблюдения аналогичны историческому эксперименту Дивера и Фэйрбэнка 1961 года. Вместо кольца они использовали сверхпроводящий цилиндр.