Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Часто электрон внешней оболочки, не находящий себе ковалентной связи, немного усиливает три связи своих собратьев с электронами соседних атомов. Вместо того чтобы упаковываться с другими слоями в трехмерный графит, слой графена деформируется, переставая быть плоским, и спонтанно образует необычные структуры. Опишем некоторые из них.

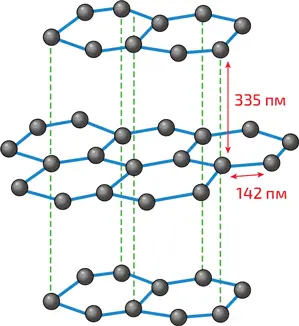
4. Структура графита. Графит состоит из совокупности слабо связанных между собой слоев графена. Эти слабые связи изображены пунктиром

В результате наблюдений и анализа исследователи в разных частях мира пришли к выводу, что в саже и пламени свечи появляется небольшое количество специфического вещества, молекулы которого состоят из 60 атомов углерода (C 60 ). Атомы углерода в нем связываются так, что образуют 20 шестиугольников и 12 пятиугольников, воспроизводя таким образом форму футбольного мяча (илл. 5a).

Впоследствии, после открытия молекулы C 60 , в природе были обнаружены или синтезированы и другие, более крупные, молекулы, также состоящие из шести- и пятиугольников. Так, например, молекула C 70 скорее имеет форму мяча для регби: она состоит из 25 шестиугольников и 12 пятиугольников (илл. 5b). К таким молекулам относится и гигант C 540 (илл. 6), который довольно легко получается путем испарения графита посредством облучения лазерным импульсом или дугового разряда. Такие молекулы, возможно, могут входить в состав межзвездной пыли.

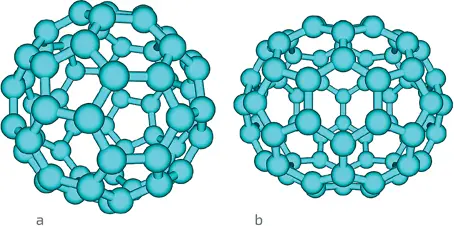
5. a.Молекула C 60 воспроизводит форму футбольного мяча, который состоит из кожаных пяти- и шестиугольников. b.Молекула C 70 отдаленно напоминает мяч для регби

Все эти молекулы, принимающие форму выпуклых многогранников и имеющие формулу C 2 n , где n – целое число, могут содержать разное число шестиугольников, но всегда 12 пятиугольников. Как это объяснить? Докажем, что в предположении, что все грани являются шести- и пятиугольниками, количество последних обязательно должно быть равно 12.

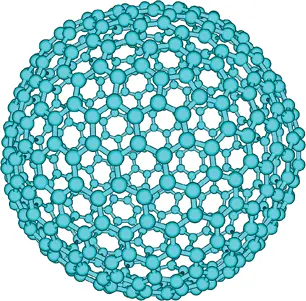
6. Молекула C 540

Пусть h – количество шестиугольников и p – пятиугольников. Согласно справедливой для многогранников теореме Эйлера, при условии, что выпуклый многогранник имеет f граней, s вершин и a ребер, эти три числа должны удовлетворять формуле:

f + s = a + 2.

Числа f, s и a легко находятся из количества шести- и пятиугольников, h и p соответственно. Прежде всего очевидно, что f = h + p . И поскольку каждый шестиугольник имеет шесть ребер, каждый пятиугольник их имеет пять, а каждое ребро является общим для двух сторон, то находим, что a = (6 h + 5 p )/2. Для нахождения числа вершин s следует заметить, что каждая из них является общей для трех граней: соединить их большое число в вершине не представляется возможным, а принять s = 2 – абсурдно. Каждый шестиугольник имеет шесть вершин, каждый пятиугольник – пять, а каждая вершина является общей для трех сторон, и, следовательно, s = (6 h + 5p )/3. Подставляя значения, найденные по формуле Эйлера, получим p = 12. Заметим, что существует многогранник с 12 пятиугольниками и совсем без шестиугольников – правильный додекаэдр, который соответствует молекуле C 20 , самой маленькой в этом семействе. Что касается того, что все грани или шести-, или пятиугольные, это неудивительно: к примеру, квадратная грань бы требовала, чтобы две связи C–C образовывали между собой прямой угол, в то время как внешние электроны, как правило, распределяются в пространстве вокруг атомов симметрично.

Молекулы, которые мы только что описали, называются фуллеренами в честь американского архитектора Бакминстера Фуллера, создателя геодезических куполов, напоминающих молекулу C 60 (которая была обнаружена первой; ее еще называют footballen из-за сходства с футбольным мячом). По сей день физики находят и исследуют потрясающе красивые структуры, созданные природой и обычно скрытые от нас, а ведь некоторые художники их предсказали! Великий тосканский художник Пьеро делла Франческа (умерший в возрасте почти 80 лет в 1492 году), вероятно, был первым, кто изобразил футбольный мяч – или, вернее, усеченный икосаэдр, полученный в результате усечения обычного икосаэдра по пяти плоскостям (см. главу 8, «Поцелуи» шаров в задаче Кеплера»). Пьеро делла Франческа увлекался математикой. Рисунок усеченного икосаэдра был обнаружен не в его «Книжице о пяти правильных телах» ( Libellus de quinque corporibus regularibus ), а в труде, опубликованном в 1510 году одним из его учеников, Лукой Пачоли. Иллюстратором книги, озаглавленной Divina Proportione («Божественная пропорция»), был… Леонардо да Винчи (илл. 7)!