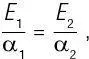Скотт Бембенек - Механизм Вселенной - как законы науки управляют миром и как мы об этом узнали

Интересный сопутствующий факт: по-видимому, атмосфера над поверхностью Солнца содержит, в частности, горячие пары натрия, которые поглощают некоторую долю излучения, идущего из ядра Солнца, приводя в результате к появлению двух линий D натрия, которые при прохождении через пламя с натрием становятся даже темнее. Таким образом, эти эксперименты также сообщают что-то об атмосфере Солнца, находящейся примерно в 93 миллионах милях от Земли.

Кирхгоф перешел к формулировке соотношения между интенсивностью излучения объекта и количеством энергии, поглощенной им на определенной частоте, когда он находится в состоянии теплового равновесия. Закон Кирхгофа и задачи, которые были поставлены Кирхгофом в результате, привели теоретиков, как и экспериментаторов, к революции в физике, которая в конечном счете достигла кульминации в квантовой механике . Возможно, нам стоит пристальнее рассмотреть эту провоцирующую теорию.

С хорошей точностью, когда вы помещаете еду в духовку и нагреваете ее до определенной температуры, а духовка достигает этой температуры и впоследствии ее поддерживает, система (еда и духовка) в конечном итоге приходит в тепловое равновесие. Допустим, мы поместили индейку в духовку и нагрели ее до 400 °F (204 °C). Как только температура достигла этих градусов и поддерживается некоторое время, мы можем утверждать (для наших целей), что духовка и индейка находятся в тепловом равновесии.

Далее, как мы говорили ранее, мы ожидаем, что индейка и внутренние стенки духовки испускают и поглощают тепловое излучение. Но это вовсе не означает, что индейка станет светиться красным, как электрический нагревательный элемент духовки; материалы все-таки разные. Тем не менее она излучает и поглощает — преимущественно в инфракрасной области спектра, которую мы не можем увидеть просто своими глазами. Поскольку тепловое равновесие установилось, индейка излучает с той же скоростью, что и поглощает. То же самое относится к внутренним стенкам духовки и всему тому, что мы туда добавляем и чему позволяем достичь теплового равновесия. Итак давайте добавим печеную картошку и доведем ее до теплового равновесия. Сфокусируемся только на индейке и картошке.

Чтобы упростить рассуждение и сосредоточить наше внимание на индейке и картошке — вещах, находящихся внутри духовки, — давайте заменим духовку «ящиком», который способен поддерживать желаемую температуру всего, что находится внутри. Более того, давайте сделаем стенки такими, что они ни поглощают, ни излучают сами, а идеально отражают излучение индейки и картошки. Вследствие этого излучение и поглощение затрагивает лишь индейку и картошку. Понимание закона Кирхгофа требует от нас понимания двух вещей:

• Часть энергии теплового излучения, испущенного индейкой, приходится на полное количество энергии теплового излучения, поглощенного картошкой, и наоборот [169].

• Вследствие теплового равновесия и индейка, и картошка будут излучать тепловую энергию в том же темпе, в котором они будут ее поглощать [170].

Эти положения, записанные математически, означают [171]:

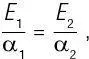
где E — количество энергии, испущенной объектом в единицу времени (это темп излучения , или излучательная способность ), α — доля энергии, поглощенной объектом, а подстрочные индексы обозначают объекты (например, 1 — индейка, 2 — картошка).

Представим идеальный объект, поглощающий все падающее на него тепловое излучение независимо от частоты. Это означает, что α = 1, то есть 100 % излучения, падающего на идеальный объект, поглощается. Такое тело по цвету абсолютно черное, так его и называют — абсолютно черное тело (АЧТ). Как мы уже знаем, объект, поглощающий на данной частоте, должен также излучать на ней (при подходящих условиях, например будучи нагретым). В случае нашего абсолютно черного тела мы утверждаем, что, когда оно нагрето (аналогично натрию, помещенному в пламя), оно будет излучать свой спектр — на всех частотах.

Таким образом, если один объект в нашей системе — абсолютно черное тело — скажем, им мы заменим картошку, тогда наше уравнение примет вид:

E 1/ α 1= E АЧТ,

и поскольку не имеет значения, каковы точные характеристики других объектов (индейки, картошки и т. п.), мы можем убрать подстрочные индексы в левой части равенства и просто записать: