Александр Китайгородский: Кристаллы

Однако некоторая свобода выбора в расположении элементарной ячейки всегда имеется. Так, совершенно безразлично, поместим ли мы углы ячейки в местах «головок» или «хвостиков» фигурок или же где-либо на белом поле между ними. В случаях 14 или 15 выбор ячейки несколько лучше подчёркивает симметрию обоев, чем, скажем, в случае 8 , но сути дела это не меняет, и мы можем, если желаем, произвольно переместить углы ячейки в случае 8 , оставляя, конечно, размеры ячейки теми же и стороны её параллельными самим себе.

Способы заполнения элементарной ячейки отдельными фигурками во всех случаях различны. Этим прежде всего и отличаются друг от друга изображённые 17 случаев. Таким образом, художник, выполнивший повторяющийся рисунок обоев, должен указать, кроме того, каким из 17 способов надо построить обои из его рисунка. Например, для случая 8 надо выполненный рисунок расположить в заштрихованной части (одной четверти) элементарной ячейки и отразить его в двух «зеркалах» (рис. 14).

17 типов симметрии плоского узора не исчерпывают, конечно, всего разнообразия узоров, составляемых из одной и той же фигурки: художник должен указать ещё одно обстоятельство, – как расположить фигурку по отношению к граничным линиям ячейки. На рисунке 14 показаны два узора обоев с той же исходной фигуркой, но различно расположенной по отношению к зеркалам. Оба эти узора относятся к случаю 8 .

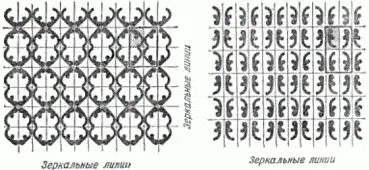
Рис. 14. Два разных расположения фигурок при одинаковом типе симметрии узора.

Мы не станем приводить правила построения обоев во всех остальных случаях.

Какое же отношение имеют обои к кристаллу?

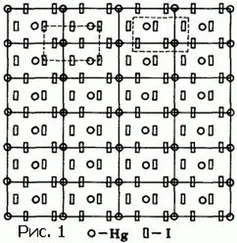
Каждое тело, в том числе и кристалл, состоит из атомов. Простые вещества состоят из одинаковых атомов, сложные – из атомов двух или нескольких сортов. Предположим, что мы могли бы в сверхмощный микроскоп рассмотреть поверхность кристалла поваренной соли и увидеть центры атомов. Рисунок 15 показывает, что атомы расположены вдоль грани кристалла, как узор обоев.

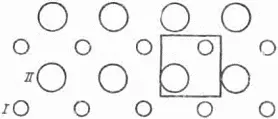
Рис. 15. Схема расположения атомов натрия (I) и хлора (II) на грани куба кристалла каменной соли.

Теперь мы готовы к тому, чтобы понять, как построен кристалл. Кристалл представляет собой «пространственные обои» . Пространственные, то есть объёмные, а не плоские элементарные ячейки – это «кирпичи», прикладыванием которых друг к другу в пространстве строится кристалл.

Сколько же способов построения «пространственных обоев» из элементарных кусков? Эта сложная математическая задача была также решена Е.С. Фёдоровым. Он доказал, что должны существовать 230 способов построения кристалла или, как сейчас говорим, 230 фёдоровских групп. Открытие Е.С. Фёдорова принадлежит к величайшим достижениям русской науки. Начатые примерно через 20 лет после вывода Фёдорова опытные проверки его теории – они стали возможными лишь после открытия рентгеновского структурного анализа – привели к блестящему её подтверждению. Не было найдено ни одного кристалла, который не принадлежал бы к той или иной фёдоровской группе.

Все современные данные о внутреннем строении кристаллов получены при помощи рентгеновского структурного анализа , открытого в 1912 году.

Маленький, размером 0,5–1 мм, кристаллик ставится на пути узкого рентгеновского луча. За кристаллом помещается фотопластинка. Наряду с прошедшим сквозь кристалл лучом возникает ряд отклонённых лучей. Мы не будем здесь останавливаться на причине их возникновения. Явление это носит название дифракции .

Проявленная фотопластинка обнаруживает много пятен, по расположению и интенсивности которых можно судить о структуре кристалла. Примерный вид такого снимка – рентгенограммы топаза – приведён на рисунке 16 (в действительности пятна обычно несколько размыты и различаются не столько по величине, сколько по яркости); справа внизу указаны размеры кристаллика. Расшифровка рентгенограмм представляет собой сложную задачу.

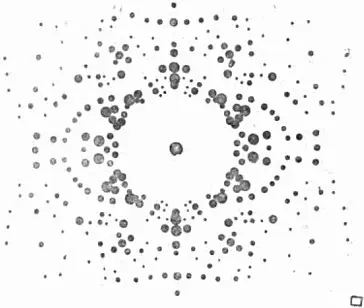
Рис. 16. Рентгенограмма кристалла топаза.

Огромное значение для развития рентгеноструктурного анализа имели труды известного русского кристаллографа Г.В. Вульфа. За время, протекшее после открытия рентгеноструктурного анализа, этим методом было изучено строение многих тысяч кристаллов.