Оказывается, есть. Сосуд этот создан французским физиком Мариоттом (помните закон Бойля – Мариотта?) и назван в его честь сосудом Мариотта. Это бутыль с узким горлом, через пробку которой вставлена стеклянная трубка (рис. 207). Если открыть кран 3 ниже конца трубки, то жидкость будет литься из него с одним и тем же напором, пока уровень воды в сосуде не опустится до нижнего конца трубки (на уровне пробки 2). Вдвинув трубку вниз почти до уровня крана 3, можно заставить всю жидкость, находящуюся выше уровня отверстий, вытечь равномерно, хотя и очень тонкой струей.
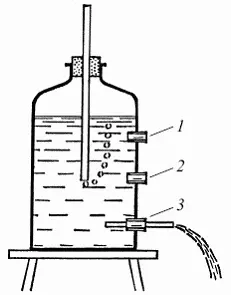
Рис. 207. Сосуд Мариотта: 1 – верхняя пробка; 2 – средняя пробка; 3 – кран
В чем же здесь дело? Проследим за тем, что происходит в сосуде при открытии крана 3. Прежде всего выливается вода из стеклянной трубки; уровень жидкости внутри нее опускается до конца трубки. При дальнейшем вытекании опускается уже уровень воды в сосуде, и через стеклянную трубку входит наружный воздух, он пробулькивает пузырьками через воду и собирается над ней в верхней части сосуда. Теперь на всем уровне пробки 2 давление равно атмосферному. Значит, вода из крана 3 вытекает лишь под давлением слоя воды 2 – 3, потому что давление атмосферы изнутри и снаружи сосуда уравновешивается. А так как толщина слоя 2 – 3 остается постоянной, то и струя течет с одинаковой скоростью.
Вот из такого бы сосуда и сделать часы в Форте Байяр! Тем более сосуд этот изобрел француз Мариотт. Разграфили бы его черточками, обозначающими, допустим, минуты и следили за прошедшим и оставшимся временем – было бы удобно!
Но в жизни все получилось бы не совсем так, как задумывалось: от пузырьков воздуха жидкость испарится, в нее попадает пыль, да и больно уж сложные часы получатся. Не лучше ли песочные часы, которые всем хороши – и герметичны, и время течет в них равномерно? Недаром мудрый старик Фура из того же форта в шоу использовал именно песочные часы.
Действительно, а почему песочные часы (рис. 208, а), в отличие от водяных, показывают ход времени равномерно? Ответ один: песок, в отличие от жидкости, истекает равномерно и формуле Торричелли не подчиняется. В чем же здесь дело?
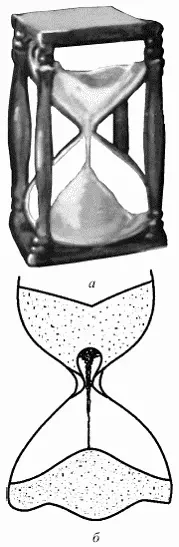
Рис. 208. Песочные часы (а) и обрушение свода в них (б)
Дело в том, что песок истекает иначе, чем жидкость, потому что в нем есть внутреннее трение. В земле можно сделать небольшой свод, и он будет держаться. Но если мы будем все более и более расширять этот свод, то он когда-нибудь обрушится, что часто бывает при добыче песка туннельным способом без крепи. Описание такого ужасного обрушения с гибелью человека есть в рассказе-триллере Леонида Андреева «Жизнь Василия Фивейского».
Если хорошо приглядеться к песочным часам, то видно, что сразу же после их перевертывания сверху высыпается чуть-чуть песка, затем в верхней колбе у отверстия образуется постоянно обрушивающийся свод (рис. 208, б), величина которого зависит, в основном, от сорта песка, обычно тщательно приготовленного по специальной технологии. А так как свод этот имеет постоянную высоту, то безразлично, имеет ли верхняя колба-трубка высоту в сантиметр, метр или километр, – давление песка у отверстия будет постоянным, поэтому и скорость вытекания песка тоже постоянна. Конечно, не точно, а почти, так как в самом начале и в самом конце процесса все происходит не совсем по писаному. Но песочные часы завоевали свое место в нашей жизни и выиграли бой с клепсидрами неспроста – их преимущества неоспоримы!
Что держит шарик на фонтане?
С течением жидкостей и газов связано много на первый взгляд таинственных и необъяснимых явлений.

Почему держится и не падает шарик на вершине фонтана и даже воздушной струи? Почему сближаются два листка бумаги или два подвешенных шарика, если подуть между ними? Почему сталкиваются идущие параллельно и близко друг к другу корабли? Почему «притягивает» близко стоящего человека быстро идущий поезд? И, наконец, почему «сама собой» поднимается жидкость в пульверизаторе или, для кого это понятнее, в карбюраторе?
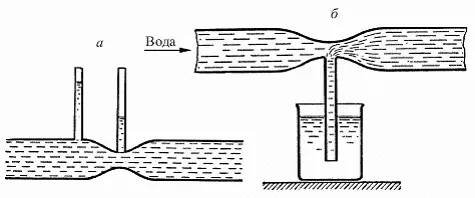
Рис. 209. Нарушение закона Паскаля в движущейся жидкости:
а – давление в узкой части трубки меньше, чем в широкой; б – вода засасывается в узкую часть трубки из стакана
Читать дальше
Конец ознакомительного отрывка
Купить книгу












