Эрик Роджерс - Физика для любознательных. Том 3. Электричество и магнетизм. Атомы и ядра

Гравитационная постоянная G = 6,67∙10 -11(ньютон∙м 2/кг 2), входящая в формулу F= G∙ M 1∙ M 2/ d 2.

Расстояние от лаборатории до центра Земли ~= 6,34∙10 6м.

Масса Земли ~= 6,0∙10 21т ~= 6,0∙10 24кг.

Используя формулу закона всемирного тяготения, вычислите приближенно силу, с которой Земля притягивает пробную массу 1 кг вблизи поверхности Земли. Это и есть напряженность гравитационного поля Земли в данной точке.

в) Воздушному шарику, диаметр которого 0,2 м (радиус 0,1 м), сообщают заряд 1 микрокулон, т. е. 1∙10 -6кулон. (Это большой заряд для такого шарика.) Вычислите напряженность электрического поля на расстоянии 0,5 м от центра шарика. Постоянная , входящая в формулу закона обратной пропорциональности квадрату расстояния для силы взаимодействия зарядов, равна 9∙10 9(ньютон∙м 2/кулон). (Постоянная появляется вместо G .)

г) Вычислите напряженность электрического поля на расстоянии 1,0 м от центра шарика.

д) Когда мы имеем дело с электрическим полем в пространстве между двумя параллельными пластинами (таким полем пользовался Милликен при измерении заряда электрона, оно используется в электронно-лучевых трубках для отклонения пучка электронов)г мы исходим из опытных данных о том, что это поле однородно. Это значит, что поле имеет одинаковую напряженность всюду в пространстве между пластинами и направлено прямо от одной пластины к другой перпендикулярно пластинам. Если мы знаем напряжение между пластинами (допустим, что к пластинам подключен вольтметр параллельно батарее, подсоединенной к пластинам для создания поля), то мы можем вычислить поле, как в следующем примере. Предположим, что разность потенциалов между двумя параллельными пластинами, отстоящими друг от друга на 0,4 м, равна 15 000 в.

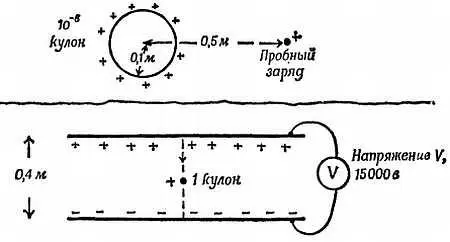
Фиг. 126. К задаче 16.

1) Разность потенциалов 15 000 в между пластинами означает, что…

Дополните эту фразу.

2) Исходя из 1) , вычислите энергию, сообщаемую электрическим полем 1 кулону, проходящему от одной пластины до другой, в джоулях.

3) Предположим, что 1 кулон, помещенный в поле в качестве пробного заряда, испытывает силу X ньютонов (т. е. предположим, что напряженность поля между пластинами равна X ньютон/кулон). Представим себе, что эта сила движет кулон от одной пластины до другой. Какое количество энергии будет таким образом сообщено кулону? (Обратите внимание, что оно в точности равно произведению СИЛА∙ПУТЬ.)

4) Напишите уравнение, из которого следует, что в 2) и 3) в ответе получается одна и та же величина. Решите это уравнение и найдите напряженность поля X .

Задача 17. Задачи с применением математического анализа. (Эти задачи имеют важное значение для изучения атомной физики.)

Чтобы детально разработать любую картину строения атома, вроде простой модели Бора, необходимо знать потенциальную энергию отрицательного электрона на расстоянии r от положительного ядра. (Точно так же, попытавшись рассчитать орбиту планеты, мы столкнемся с необходимостью определить потенциальную энергию тела в гравитационном поле.) Для этого нам нужно знать разность потенциалов V между бесконечностью и точкой, удаленной от заряда ядра Q на расстояние r . Если заряд +1 кулон при перенесении его из бесконечности в точку, удаленную от ядра на r , приобретает электрическую потенциальную энергию V дж, то электрон с зарядом е приобретает энергию V ∙ e дж. Поскольку е отрицательно и равно —1,6∙10 -19кулон, электрон при переводе его из бесконечности на орбиту с радиусом r теряет потенциальную энергию. Вот почему электрон не может покинуть орбиту, пока ему не будет сообщена добавочная энергия путем бомбардировки. Итак, вы найдете выражение для V , которым пользуются в атомной физике. Оно получается в результате вычисления работы, совершаемой против силы отталкивания ∙ Q(1)/ d 2при перенесении +1 кулон из d = бесконечности в d = r . Сила отталкивания меняется с изменением расстояния d , поэтому определить V простым перемножением СИЛА∙ПУТЬ нельзя. Вместо этого мы должны разбить весь путь на очень короткие участки, вычислить работу на каждом участке и сложить результаты. Разбивая путь на все более короткие участки, мы получим в пределе то, что дает метод математического анализа, называемый интегрированием, (Существуют приемы, позволяющие проделать этот расчет без помощи математического анализа, однако каждый, кто в состоянии проследить за подобными выкладками, смог бы за это время познакомиться с математическим анализом, доставив себе большое удовольствие.) Приведем вывод формулы математического анализа, заменив букву d на х .