Эрик Роджерс - Физика для любознательных. Том 3. Электричество и магнетизм. Атомы и ядра

Вспомните, что решетка разделяет свет на составляющие по длинам волн, и это разделение показывает, что у красного света длина волны примерно вдвое больше, чем у голубого.

Простую гармоническую волну характеризуют три величины:

I) длина волны, λ — расстояние от одного гребня до другого;

II) частота f — число полных длин волн, прошедших мимо наблюдателя в секунду, или число колебаний источника в секунду, или число колебаний любого датчика (в секунду), на который, проходя мимо него, действует волна;

III) скорость v , с которой перемещается профиль волны.

За 1 сек профиль волны смещается на расстояние v , а мимо исходной точки проходит f таких профилей длиной λ . Следовательно, v= f∙ λ.

СКОРОСТЬ = ЧАСТОТА ∙ (ДЛИНА ВОЛНЫ)

для любой периодической волны.

Для света в воздухе или вакууме и— универсальная величина 3∙10 8м/сек, которую мы обозначаем буквой с . Обозначим еще частоту через v вместо f ( v — буква греческого алфавита, аналогичная русской «н», читается «ню»). Тогда c= v∙ λ, и частота v= c/ λ. Поскольку с — постоянная, частота обратно пропорциональна длине волны . Чем меньше длина волны, тем больше частота. Приведенная ниже таблица грубо показывает некоторые значения этих величин.

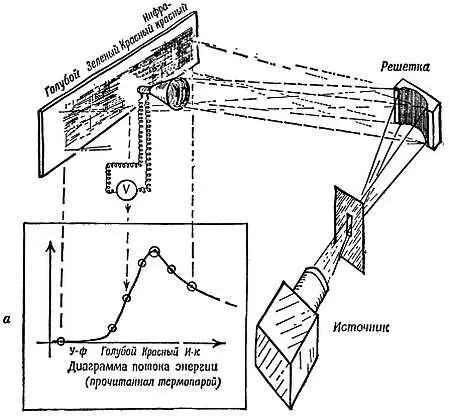
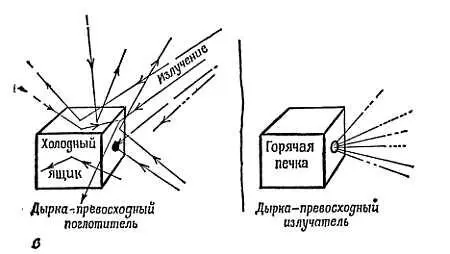
Фиг. 173. Энергетический спектр излучения.

а— экспериментальное устройство; б— детали термопары; в— дырка — превосходный излучатель типа «черного тела».

Обратимся к теории и посмотрим, что она предсказывает для такого графика, если исходить из знания других отраслей физики.

Надежные термодинамические аргументы приводят к некоторым вполне определенным предсказаниям о полном излучении «черного тела» при различных температурах:

1. Закон Стефана:

(ПОЛНЫЙ ПОТОК ЭНЕРГИИ во всем спектре) ~ (АБСОЛЮТНАЯ ТЕМПЕРАТУРА ИЗЛУЧАТЕЛЯ) 4

или

E~ T 4

2. Закон Вина:

Длина волны λ макс, на которую приходится максимум графика, показывающего зависимость энергии излучения от длины волны, обратно пропорциональна абсолютной температуре, так что

λ макс∙ T= Const .

Эксперименты подтверждают справедливость этих законов вплоть до наибольших энергий, которые можно измерить газовым термозвезд по шкале Кельвина. Оба закона дают одинаковую температуру поверхности Солнца примерно 6000° К.

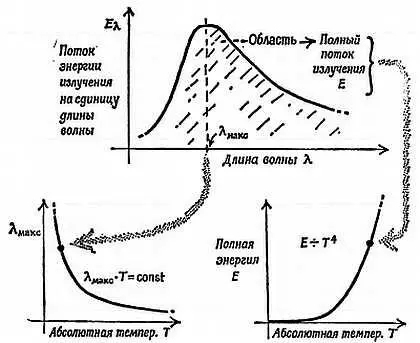
Фиг. 174. Излучение (экспериментальные факты).

Но дальнейшее рассмотрение на основе традиционной [185](ньютоновской) механики предсказывает также детальную форму графика, и она оказывается совершенно неверной. Это предсказание в вопиющем противоречии с фактами гласит: обмен энергией внутри печки должен приводить к передаче энергии от любой длины волны к более короткой до тех пор, пока практически вся энергия не окажется в ультрафиолете или еще дальше . Таким образом, на предсказанном графике кривая стремится к бесконечности в области ультрафиолета. Разумеется, эта «ультрафиолетовая катастрофа» не наблюдается у реальных излучателей, от разогретого докрасна железа до ярко-белого Солнца. Они излучают тепло в виде оранжевого света вместо того, чтобы остывать из-за быстрой ультрафиолетовой вспышки. Физики делали повторные попытки вывести экспериментальное энергетическое распределение из обычной волновой теории, уравнений Максвелла и электронной теории. Всех постигала неудача: снова и снова предсказания хорошо совпадали с экспериментом на красном конце спектра, но на другом конце возникала ультрафиолетовая катастрофа. Тогда около 1900 г. немецкий физик Макс Планк подошел к проблеме с другой стороны и спросил, как Эйнштейн в теории относительности (исторически позже. — Перев .): как нужно минимально модифицировать теорию, чтобы согласовать ее с фактами? Он располагал только экспериментальной кривой, но не ее алгебраической формулой, поэтому и не мог с помощью логики найти точную модификацию. Вместо этого Планк обратился к догадкам и предположениям, как в свое время поступил Кеплер. После блестящего умозрительного анализа он нашел успешное правило. Планк заметил, что необходимо некоторое правило, которое бы оставляло красный свет практически неизменным, но подавляло фиолетовое и ультрафиолетовое излучение. Рассмотрим аналогичную задачу в большом бакалейном магазине. Как можно ограничить продажу каких-либо товаров, не повышая цены на них? Можно было бы продавать товары только большими партиями. Например, для распределения в семье денег на покупки не имеет особого значения, что рис, сахар и соль продаются не вразвес, а в пакетах по полкилограмма. Но если сахар упакован в неделимые мешки по 50 кг, то его будут покупать только те семьи, в которых есть сильные руки, большой автомобиль и другие ресурсы. Торговля сахаром в магазине почти прекратилась бы из-за ограничений, наложенных расфасовкой в слишком большие мешки.