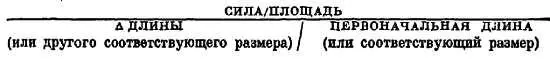Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Отсюда отношение между силой F , потребной для определенного удлинения, и площадью поперечного сечения А должно быть равно _? _ _? _.

Для проволоки круглого сечения отношение между силой F (для определенного удлинения) и диаметром d должно быть равно _? _ ~ _? _.

Задача 8

Отношение (растягивающая сила)/(площадь поперечного сечения) действительно определяет удлинение для данного материала. Мы называем это отношение напряжением. Тогда, если одинаковое напряжение приложено к проволокам разных диаметров, но одной и той же длины и сделанным из одинакового материала, удлинение для всех этих проволок должно быть одинаковым.

Объясните кратко, почему: ___

Задача 9

В пределах области действия закона Гука удвоение длины проволоки дает как бы две проволоки, каждая из которых будет растягиваться с первоначальным удлинением. Таким образом, общее удлинение при той же нагрузке будет в ___ раз больше.

Вообще отношение между удлинением Δl и длиной l проволоки для нескольких разных проволок из того же материала, несущих одинаковую нагрузку, будет ___.

Задача 10

Рассматривая поведение проволоки различной длины, мы видим, что отношение (удлинение)/(длина) должно быть одинаковым для всех проволок из одного и того же материала при том же напряжении, хотя длина проволок различна. Считаете ли вы это утверждение рискованным? приемлемым? по-видимому, правильным? правильным? ___

Это отношение называется деформацией. Пользуясь им, мы можем отвлечься от длины образца и установить характеристику самого материала. Если мы измеряем удлинение и длину в миллиметрах то деформация должна измеряться в ___ (единицы).

Задача 11

Инженерам и физикам часто бывает необходимо знать упругие свойства материала в определенном виде, пригодном для разнообразных форм и размеров образцов и разнообразных прилагаемых сил. С этой целью мы используем:

напряжение, которое представляет собой отношение

СИЛА/ПЛОЩАДЬ (к которой она приложена)

вместо собственно силы (нагрузки);

деформацию, представляющую собой отношение

ИЗМЕНЕНИЕ ДЛИНЫ (или соответствующего размера)/ПЕРВОНАЧАЛЬНАЯ ДЛИНА (или соответствующий размер)

вместо собственно изменения длины.

Тогда в пределах действия закона Гука, где простейшим утверждением является

УДЛИНЕНИЕ ~ НАГРУЗКА [или (НАГРУЗКА)/(УДЛИНЕНИЕ) = соnst ],

мы получаем более обобщенное отношение, которое, подобно отношению (нагрузка)/(удлинение), постоянно. Но это обобщенное отношение не зависит ни от формы, ни от размера используемого образца. Оно одинаково для всех образцов данного материала. Чтобы вывести обобщеннов отношение, мы используем напряжение и деформацию вместо нагрузки и удлинения. Теперь мы можем представить закон Гуна в общей, итоговой форме:

?/? = const

Эта постоянная называется модулем. Чем легче вещество растягивается (или сжимается), тем

___________ должен быть его модуль.

(больше?/меньше?)

Используя напряжение и деформацию, можно представить закон Гука в общей форме: ( напряжение )/( деформация ) = const ; это значит, что отношение

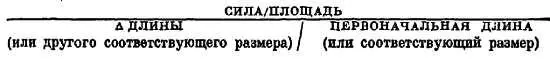
постоянно.

Такое отношение ( напряжение )/( деформация ) мы называем модулем .

В пределах справедливости закона Гука модуль является характеристикой материала, различной для различных видов деформации, но не зависящей ни от формы, ни от размеров образца и приложенной силы. Чем больше сила, необходимая для придания материалу заданной деформации, тем больше модуль. Следовательно, величина модуля характеризует жесткость материала, а не легкость его растяжения и т. п.

Для чистого растяжения стержня или проволоки с помощью растягивающей силы (мы об этом говорили) модуль, определяемый отношением ( напряжение )/( деформация ), называется модулем Юнга (модуль продольной упругости). Он относится также и к сжатию (фиг. 104, а ). Инженеры пользуются им, чтобы заранее определять возможные изменения мостовых балок при их растяжении или сжатии.

При изгибе упругой балки одни волокна растягиваются, другие сжимаются (фиг. 104, б ), поэтому модуль Юнга применяется и при изгибе. Пометьте резиновую трубку или резиновый брусок чернилами и постарайтесь растянуть или изогнуть их.