Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

в) Покажите с помощью рисунков и краткого описания, как правило параллелограмма для сложения векторов (т. е. правило геометрического сложения) ведет к способу многоугольника, при котором каждый последующий из складываемых векторов проводится из конца предыдущего.

Задача 6. Важное соотношение: груз на наклонной плоскости

Тело покоится на наклонной плоскости без трения; наклонная плоскость образует с горизонтальным направлением угол А (отношение высоты наклонной плоскости h к длине L таково, что sin A = h/ L). Тело удерживается на наклонной плоскости от скольжения вниз веревкой, натяжение которой F параллельно наклонной плоскости. Земное притяжение действует на тело вертикально вниз с силой, которую мы называем весом тела W (фиг. 78).

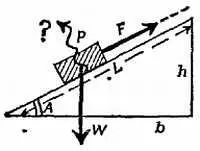
Фиг. 78. К задаче 6.

а) Изобразите тело на наклонной плоскости и укажите стрелками направления W и F . Добавьте еще одну стрелку и укажите направление реакции опоры Р , с помощью которой наклонная плоскость действует на тело. Считайте, что, поскольку трение на наклонной плоскости отсутствует, реакция опоры Р должна быть перпендикулярна к поверхности наклонной плоскости. Покажите все ото стрелками, выходящими из тела.

б) Начертите еще один рисунок, показывающий, что векторы, W, Р и F при сложении дают нуль.

в) Если вы согласны, что оба ваши рисунка содержат подобные треугольники, то, воспользовавшись этим, выразите отношение F / W через h и через угол А .

г) Представьте себе теперь, что веревку перерезали так, что сила F исчезает и тело начинает двигаться с ускорением вниз по наклонной плоскости.

В отсутствие веревки на тело действует результирующая сила, направленная вниз по наклонной плоскости, такой же величины, как сила F , которая была направлена вверх по наклонной плоскости. Какова величина этой силы?

Задача 7

Рассмотрите задачу 6 другим способом. Разложите вес W на компоненты F (направлена вниз по наклонной плоскости) и Р (направлена перпендикулярно к наклонной плоскости). Выразите F через W u h и т. д. Это позволяет найти необходимое натяжение веревки и, если веревка отсутствует, — результирующую силу, направленную вниз по наклонной плоскости, которая вызывает ускоренное движение тела.

Задача 8

Незадолго до работ Галилея Стевин опубликовал остроумный «мысленный» эксперимент. Он рассуждал следующим образом. Представим себе связку гладких шариков в виде ожерелья, повешенную на треугольную призму (фиг. 79).

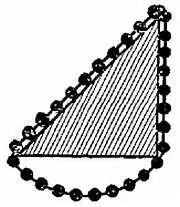
Фиг. 79. К задаче 8.

Связка должна находиться в равновесии: мы не предполагаем, что она, скользя по наклонной плоскости, будет двигаться вокруг призмы все быстрее и быстрее, просто потому, что на наклонной плоскости больше шариков.

Отрежем с двух концов ту часть связки, которая свободно свешивается под призмой. Поскольку эта часть связки симметрична, ее удаление не может нарушить равновесия. Исходя из этого, Стевин предсказал, что отношение F / W для груза на наклонной плоскости должно быть равно h / L . Попытайтесь продолжить и завершить его рассуждения и прийти к этому выводу. ( Указание . Сосредоточьте все шарики, находящиеся на наклонной плоскости, в один сплошной кусок, а все шарики, висящие вертикально, — в другой кусок. Соедините оба куска нитью, перекинутой через блок.)

Задача 9

Конструктор намерен включить в свой прибор маятник, груз которого оттягивался бы в сторону шнуром, перпендикулярным к нити маятника, т. е. направленным по касательной к дуге, описываемой грузом (фиг. 80). Длина нити маятника 3 м, железный груз весит 10 кГ.

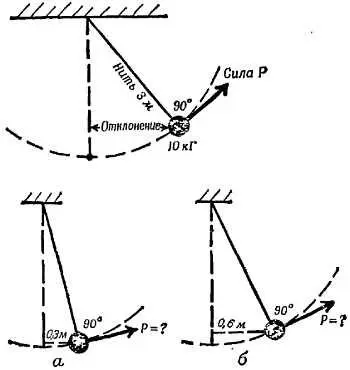
Фиг. 80. К задаче 9.

а) Какую силу Р нужно приложить к грузу маятника, чтобы оттянуть его на 0,3 м по горизонтали? Аккуратно постройте диаграммы и сопроводите ваши расчеты объяснениями.

б) Повторите расчет при условии, что груз оттягивается в сторону на 0,6; 0,9; 1,2; 1,5 м по горизонтали.

в) Что вы можете вообще сказать относительно силы Р , необходимой, чтобы сообщить грузу такие отклонения? (В этом заключается исходное положение теории колебаний маятника.)