Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Масштаб: в 1 см — 0,5 м; в 1 см — 1 кГ.

Проводим вертикальную прямую и откладываем на ней направленный вниз вектор АВ длиной 2 см, обозначающий вес птицы 2 кГ. Из точки В проводим отрезок ВС , параллельный правой стороне провода, обозначающий натяжение провода, затем — еще один вектор, параллельный левой половине провода. Этот вектор должен замкнуть треугольник, поскольку сумма сил, действующих на Y , должна быть равна нулю, Но мы не знаем, какой длины должны быть векторы натяжений. Поэтому проводим две прямые: одну из точки В вверх под углом Е , а вторую — через точку А , также под углом Е , и отмечаем точку С пересечения этих прямых. Теперь у нас есть треугольник сил, стороны которого можно было бы измерить и определить, исходя из выбранного масштаба.

Можно обойтись и без измерений, если удастся увязать диаграмму сил с реальной конфигурацией посредством подобных треугольников (фиг. 75).

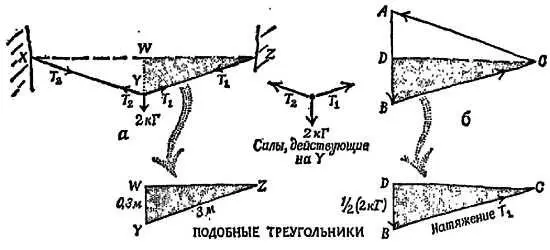
Фиг. 75. Применение теоремы о подобных треугольниках.

а— схема приложения сил; б— диаграмма сил (все не в масштабе).

Треугольник сил ABC не подобен треугольнику XYZ , но, как в большинстве таких задач, можно отыскать подобные треугольники, произведя простые дополнительные построения. В данном случае можно провести линии, показанные на фигуре пунктиром, и воспользоваться доказательством, данным ниже.

Треугольники WYZ и DBC подобны. В треугольнике DBC сторона DB представляет собой половину веса птицы, т. е. 1/ 2(2 кГ).

В треугольнике WYZ сторона WY представляет собой вертикальный провес провода, равный по условию 0,3 м.

Таким образом,

3 м/0,3 м в треугольнике WYZ = Т 1кГ/1 кГ в треугольнике DBC .

Отсюда натяжение Т 1= (1 кГ)(10/1) = 10 кГ. Точно так же находим Т 2 = 10 кГ.

Птица весом 2 кГ способна создать натяжение 10 кГ. Как вы думаете, каково было бы натяжение, если бы провод не был так слабо натянут и провисал не на 0,3 м, а всего на 2 см?

Задача 2

Маятник состоит из груза весом 6 кГ, подвешенного на веревке длиной 3 м. Груз оттянут в сторону приложенной к нему горизонтальной силой. При этом натяжение веревки маятника, составляющей некоторый угол с вертикалью, равно 10 кГ.

а) Какова величина горизонтальной силы, приложенной к грузу?

б) Какой угол составляет с вертикалью нить маятника?

Задача 3

Хирург накладывает на плечо больного специальную шину и хочет приложить к ней вертикальную направленную вниз силу 5 кГ. Он предлагает для этого оттянуть шину вниз с помощью веревки. Чтобы плечи и грудная клетка больного не создавали при этом помехи, хирург осуществляет натяжение шины двумя веревками, идущими от плеча по обе стороны, спереди и сзади, причем каждая веревка образует угол 30° с вертикалью (фиг. 76).

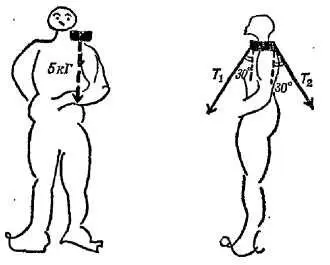
Фиг. 76. К задаче 3.

а) Вычислите необходимое натяжение каждой веревки. (Постройте в большом масштабе наглядную диаграмму сил.)

б) Объясните проведенные вами вычисления.

Задача 4

Канатоходец, весящий 75 кГ, стоит посредине каната длиной 8,6 м, натянутого между двумя опорами, отстоящими друг от друга на 8 м (фиг. 77, а ).

а) Найдите натяжение каната, сопроводив вычисления диаграммами и четкими объяснениями. ( Примечание . При указанных размерах провес посредине составляет 1,7 м.)

б) Представьте себе, что канат удлинен с одной стороны и прикреплен к более высокой опоре, как показано на фиг. 77, б , причем углы, которые обе половины каната образуют с горизонтальным направлением, остаются прежними. Как это скажется на натяжении(ях)?

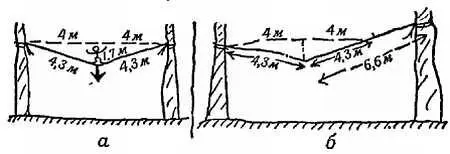
Фиг. 77. К задаче 4.

Задача 5

а) Какие из перечисленных ниже слов должны, по вашему мнению, обозначать векторы (вектор — это величина, которая подчиняется правилу геометрического сложения); сила, объем, ускорение, скорость, температура, плотность, доброта, скромность, влажность, электрическое поле?

б) Дайте (максимум в две строчки) письменное определение суммы, нескольких векторов. (Не приводите правила для нахождения суммы. Дайте ясное описание, из которого было бы видно, что это такое.)