Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

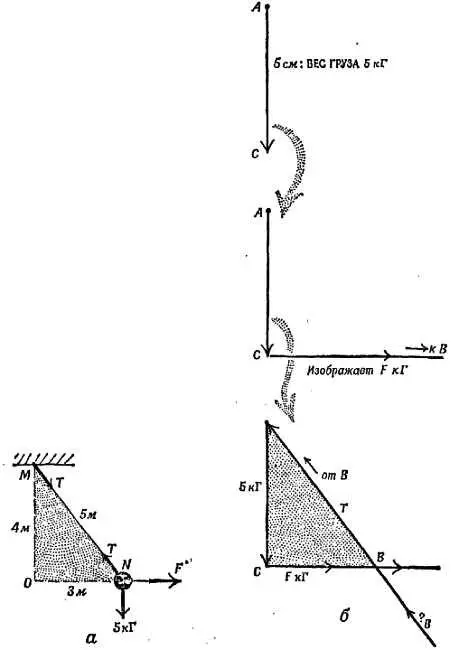
Фиг. 72. Построение диаграммы сил.

а— схема приложения сил; б— этапы построения диаграммы сил; поскольку треугольник может быть задан двумя углами и одной из сторон, построить диаграмму сил возможно.

Построение диаграммы сил мы начинаем, проведя АС , вектор единственной силы, о которой нам все известно, — силы, направленной вниз и равной весу груза 5 кГ. Теперь прибавим к ней горизонтальную силу, т. е. проведем горизонтальную прямую из конца вектора АС . Но величина этой силы нам пока неизвестна, поэтому мы не знаем, какой длины должен быть изображающий ее отрезок. Однако мы знаем, что, прибавив к остальным двум силам натяжение веревки маятника, мы должны получить замкнутый треугольник сил (если груз маятника находится в равновесии). Поэтому вектор силы натяжения должен выходить из конца силы F и оканчиваться в точке А . Кроме того, натяжение веревки должно быть направлено вдоль самой веревки. (Можете ли вы представить себе веревку, позволяющую тянуть в каком-то ином направлении, нежели вдоль самой веревки?) Таким образом, мы переносим направление веревки с рисунка, изображающего реальную схему, на диаграмму сил и проводим через точку А прямую, параллельную направлению веревки. Этот отрезок наклонной прямой образует третью сторону треугольника сил ВА — натяжение веревки. Угол В примыкает к прямой, проходящей наклонно, и к горизонтальной прямой, при этом он должен быть образован пересечением обеих этих прямых. Найдя положение точки В , мы узнаем величину силы F , попутно мы определили также натяжение веревки маятника. Для нахождения величины интересующей нас силы мы построили точный чертеж и произвели измерение.

В этом случае числовые данные позволяют проделать простые вычисления, исходя из геометрических соображений, и можно рассчитать F по приближенным рисункам, рассуждая следующим образом: стороны треугольника сил ABC параллельны сторонам треугольника MNО на реальной схеме, следовательно [38] Если вам еще неизвестны свойства подобных треугольников, обратитесь к какому-нибудь учебнику геометрии или попросите, чтобы вам их объяснили: необходимо уметь уверенно ими пользоваться. , эти треугольники подобны. (По теореме Пифагора находим ОМ = 1,2 м.)

Итак,

F кГ/5 кГ на треугольнике сил = 0,9 м/1,2 м

Следовательно,

F = (5 кГ)∙3/4

т. е.

горизонтальная сила F = 3,75 кГ.

Аналогично,

Т кГ/5 кГ = 1,5 м/1,2 м

Отсюда натяжение веревки маятника Т = 6,25 кГ.

Пример В

Телефонный провод натянут между двумя опорами, отстоящими друг от друга на 6 м (фиг. 73), натяжение провода невелико. На провод, как раз посредине, села птица весом 2 кГ. Средняя точка провода провисла на 0,3 м от уровня, на котором находятся крайние точки провода, прикрепленные к опорам. Вычислите натяжение провода.

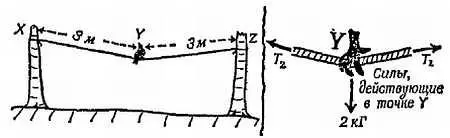
Фиг. 73. К примеру В.

(На первый взгляд эта задача может показаться надуманной, подобно множеству задач статики, однако на самом деле речь идет об очень серьезной проблеме, с которой сталкиваются при эксплуатации проводов телефонной связи и линий электропередач. Как показывает ответ на эту задачу, птицы и обледенения могут вызвать огромные натяжения в проводах, способные привести к их удлинению и даже разрыву.)

Построим диаграмму сил для небольшого центрального участка провода Y , где сидит птица [39] Откуда нам известно, что целесообразно выбрать этот кусок провода для построения диаграммы сил, а не половину провода XY или не весь провод XYZ ? Удачно выбрать для рассмотрения ту или иную часть конструкции — это один из приемов решения задач статики; этими приемами можно быстро научиться пользоваться, но для серьезной науки они не представляют большой ценности. . На этот участок провода действуют три силы: вес птицы, направленный вниз, и натяжения провода Т 1и Т 2, направленные под некоторым углом к горизонту. Угол между проводом и горизонталью назовем Е .

Построение диаграммы сил для Y (фиг. 74) начинаем с веса птицы — вполне известной нам силы.

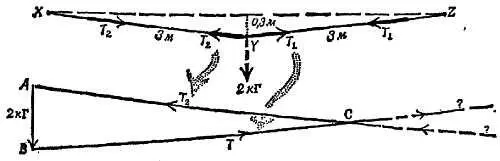
Фиг. 74. Диаграмма сил ( а) и схема приложения сил ( б).