Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Математика говорит: если ускорение a (= Δv / Δt ) постоянно и s — расстояние, пройденное за время t с этим постоянным ускорением, то

s= 1/2 at 2,

если движение начинается из состояния покоя, и

s= v 0 t+ 1/2 at 2,

если движение начинается со скоростью v 0в момент t = 0, когда включаются часы. (Логическое доказательство правильности этого «если…, то…» дается в приложении I , стр. 60.) В этих соотношениях 1/2 а — это число, поскольку мы предполагаем, что а постоянно; поэтому для движения, которое начинается из состояния покоя,

ПРОЙДЕННЫЙ ПУТЬ = (ПОСТОЯННОЕ ЧИСЛО)∙(ВРЕМЯ) 2,

или

ПРОЙДЕННЫЙ ПУТЬ возрастает прямо пропорционально (ВРЕМЯ) 2,

или

ПРОЙДЕННЫЙ ПУТЬ изменяется прямо пропорционально (ВРЕМЯ) 2,

или

ПРОЙДЕННЫЙ ПУТЬ пропорционален (ВРЕМЯ) 2[или: ~ (ВРЕМЯ) 2].

(Так сокращенно записывается любая из приведенных выше формулировок. Вместо слова «пропорционален» мы будем употреблять также знак ~.)

Например, если тело, движущееся с постоянным ускорением, проходит определенный путь за 1 сек, считая с момента начала движения из состояния покоя, то оно пройдет в 4 раза больший путь за 2 сек после начала движения из состояния покоя, в 9 раз больший путь за 3 сек и т. д.

Задача 1. График ускоренного движения

а) Предположим, что жук ползет к себе домой, совершая движение, для которого справедлива формула:

ПРОЙДЕННЫЙ ПУТЬ ~ (ВРЕМЯ) 2.

Начиная движение из состояния покоя, жук проходит за первую секунду 5 мм. Какой путь он пройдет за 2 сек от начала движения? За 3 сек? За 4, 5, 6 сек?

б) Проведите на листе бумаги прямую линию; отметьте исходную точку вблизи одного конца проведенной линии и нанесите на ней шкалу в сантиметрах. Нанесите отметки, соответствующие месту нахождения жука в конце каждой секунды.

Задача 2. Простое правило

Галилей предложил для равномерно-ускоренного движения соотношение s ~ t 2(где s — весь пройденный путь за все время t с момента начала движения из состояния покоя); он сформулировал для такого движения еще одно простое правило, связывающее расстояния d 1, d 2…, проходимые в течение следующих друг за другом односекундных интервалов, т. е, расстояние, пройденное за первую секунду, расстояние, пройденное в течение следующего интервала продолжительностью 1 сек, и т. д. Найдите такое правило в задаче 1 и сформулируйте его. ( Указание . Вычислите d 1= s 1— 0, d 2= s 2— s 1… и найдите правило, связывающее эти расстояния, проходимые за 1 сек.)

Задача 3. Научное мышление

а) Правило, о котором идет речь в задаче 2, можно было предвидеть, поразмыслив над ускоренным движением, исходя из здравого смысла и не пользуясь алгебраическими формулами или каким-либо конкретным примером.

Каким образом? ( Указание . Путь, пройденный за 1 сек., является мерой…?… за этот промежуток времени.)

б) Ограничено ли правило задачи 2 (подобно соотношению s ~ t 2) движением, начинающимся из состояния покоя при t = 0, или оно применимо к любому движению с постоянным ускорением?

Задача 4. Анализ движений

Ниже приведены данные о пути, пройденном четырьмя велосипедистами, совершившими различные по характеру движения. Все велосипедисты проходили мимо поста Р в момент пуска часов. Пройденные ими расстояния от Р спустя 1, 2, 3, 4, 5 сек даны в следующей таблице:

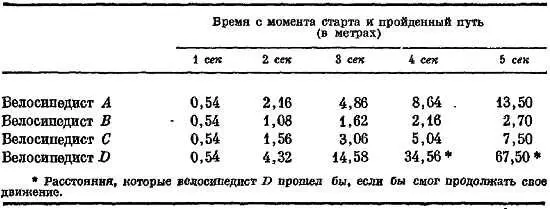
а) Попытайтесь проанализировать каждое из этих движений, проверяя постоянство ускорения не при помощи соотношения s ~ t 2, а в свете ответов на приведенные выше задачи 2 и 3.

б) Опишите, если сможете, общий характер движения, когда оно происходит не с постоянным ускорением.

Экспериментальные исследования

Можно показать, что справедливо и обратное. Если пройденный путь s прямо пропорционален t 2, то ускорение постоянно [19] Из математического анализа следует, что если s = kt 2 , то скорость ds / dt = 2 kt , а ускорение dv / dt = d / dt ( ds / dt ) = 2 k , т. е. постоянно. . Это утверждение дает нам соотношение, которое можно проверить, исследуя реальные движения. Пусть часы отсчитывают равные интервалы времени; будем измерять расстояния, которые проходит падающее тело за промежутки времени, отсчитываемые с момента начала движения из состояния покоя и находящиеся в отношении 1:2:3… Если проходимые телом расстояния будут находиться в отношении 1:4:9…, то движение происходит с постоянным ускорением. Или, как это делают в одном из лабораторных экспериментов, можно измерять время t для различных расстояний s , проходимых от начала движения, и проверить справедливость соотношения s = (постоянное число)∙( t 2) путем арифметических расчетов или построения графиков.