Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

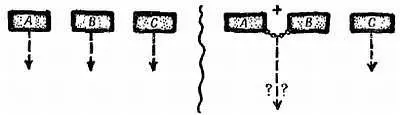
Фиг. 4. Мысленный эксперимент Галилея.

Свободное падение

Если все свободно падающие тела движутся одинаково, то это движение само по себе заслуживает детального исследования. Оно могло бы рассказать нам кое-что о природе вообще, о чем-то общем для всех падающих предметов. Свободно падающие тела движутся все быстрее и быстрее, они ускоряются. (Это слово означает лишь «движутся быстрее», употребление его не делает наше утверждение более научным.) Какого же рода ускоренное движение они совершают?

1. Возрастает ли скорость скачкообразно? Эксперимент отвечает на этот вопрос отрицательно.

2. Возрастает ли скорость в прямой пропорции к пройденному расстоянию ! Галилей путем остроумных рассуждений показал, что это весьма маловероятно [16] Доказательство Галилея было остроумным, но не вполне строгим. Суть его такова; сравним два перемещения, каждое из которых начинается из состояния покоя, — перемещение тела А на некоторое расстояние и перемещение тела В на вдвое большее расстояние. Если скорость возрастает пропорционально пройденному расстоянию, то скорости на соответствующих этапах перемещения В (половина пути, три четверти и т. д.) будут вдвое больше, чем при перемещении тела А . Значит, удвоенный путь телом В проходится с удвоенными скоростями и отнимает в целом столько же времени, сколько перемещение тела А , что абсурдно. Но это доказательство предполагает, что движение могло начаться из состояния покоя. Строгий вариант доказательства требует применения математического анализа, чтобы показать, что описанное движение никогда не может начаться из состояния покоя. Начавшись, такое движение продолжалось бы все более стремительно, и его скорость возрастала бы по закону сложных процентов.

3. Возрастает ли скорость прямо пропорционально времени ?

4. Возрастает ли она пропорционально квадрату времени ?

5. Или каким-то иным, более сложным образом?

Поскольку мы задаем вопрос о реальной природе, ответ на него могут дать только эксперименты. (Если вы хотите узнать, какого роста был Авраам Линкольн, вам придется узнать это у кого-нибудь, кто фактически измерял его рост. Сведения, почерпнутые из книг, бесполезны, если они не исходят первоначально из реальных измерений. Одна алгебра ничем не сможет вам помочь.) Мы могли бы отправиться прямо в лабораторию и упрямо экспериментировать, надеясь получить важный материал из множества измерений. Или же мы могли бы сначала все обдумать, высказать предположения относительно каких-то простых типов движения, рассчитать результаты для каждого из них, а затем проверить эти результаты в лаборатории экспериментально. Оба метода содействовали бы развитию науки.

Индуктивный и дедуктивный методы

Первый метод называют индуктивным . Мы собираем информацию либо в лаборатории, либо из накопленного багажа профессиональных знаний и затем извлекаем из этой информации простое правило или описание явлений природы. Этот процесс вывода общих положений мы называем индуктивными выводами , или просто индукцией . Сначала собираются экспериментальные данные, а затем из этих данных выводятся общие правила или законы. Так, наблюдая в течение нескольких лет за Луной, можно было бы извлечь правило, по которому Луна регулярно обращается вокруг Земли, совершая примерно 13 оборотов в год и, пользуясь методом индукции, можно прийти к уверенному выводу, что так будет продолжаться и впредь. Далее, из обширных наблюдений лунного затмения мы могли бы вывести индуктивным путем правило, согласно которому затмения Луны происходят несколькими регулярными сериями, причем в каждой такой серии затмения следуют одно за другим через постоянный промежуток времени, близкий к 18 годам.

Второй метод называют дедуктивным . Мы исходим из каких-то общих правил или представлений, а затем путем логических рассуждений выводим из них частные следствия или предсказания.

Ученые проверяют затем подобные предсказания на опыте. Если эксперимент подтверждает предсказания, то мы продолжаем развивать свою схему. Если же результаты эксперимента расходятся с нашими выводами, мы подвергаем сомнению первоначальные предположения и пытаемся видоизменить их. Например, мы могли бы предположить, что затмения Луны вызываются тем, что Земля оказывается на пути солнечных лучей и отбрасывает тень на Луну; далее мы делаем предположение о характере движения Солнца и Луны и затем путем дедукции приходим к выводу, что затмение должно снова произойти через промежуток времени, достаточный для того, чтобы Солнце и Луна вернулись в то же самое положение по отношению к Земле. Этот промежуток времени должен быть «наименьшим общим кратным» одного лунного месяца и одного солнечного года. Так, комбинируя простые наблюдения и разумные предположения, мы могли бы сделать дедуктивный вывод о восемнадцатилетнем цикле повторения затмений. (Для успешного расчета в качестве солнечного года необходимо взять особый, короткий год, связанный с меняющейся орбитой Луны.)