Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Кеплер пытался снова и снова найти простое соотношение, связывающее радиус одной орбиты с радиусом следующей. На основании наблюдений, проведенных Тихо Браге, Кеплер вычислил, что радиусы орбит в системе Коперника приближенно относятся как 8:15:20:30:115:195. Он пытался понять тайну этих отношений. Каждая догадка стоила ему немало труда, и каждый раз, когда оказывалось, что она не соответствует фактам, Кеплер честно от нее отказывался. Его мистически настроенный ум заставлял его считать, подобно древним грекам, что окружности — идеальные формы. Одно время он думал, что можно построить модель орбит, по которым движутся планеты, следующим образом: начертить окружность, вписать в нее равносторонний треугольник, затем вписать в этот треугольник еще окружность, в нее снова треугольник и т. д. Эта схема состоит из ряда окружностей, радиусы которых относятся как 2:1. Кеплер надеялся, что можно построить такие окружности, отношения радиусов которых будут соответствовать отношениям радиусов орбит, если пользоваться вместо треугольников квадратами, шестиугольниками и т. д.

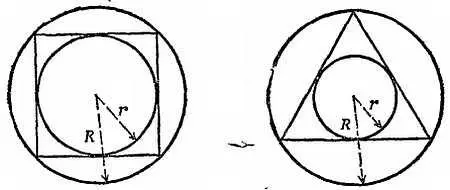
Фиг. 73. Первая гипотеза Кеплера.

В правильный многоугольник (например, квадрат) мощно вписать окружность так, чтобы она касалась его сторон. Можно также вписать окружность, проходящую через вершины квадрата. Для этой окружности можно в свою очередь построить правильный многоугольник, в который она будет вписана. Отношение радиусов R / r этих окружностей будет одинаково для всех квадратов, другое значение R / r будет иметь место для всех треугольников. Геометрическая задача : каково будет отношение R / r для внутреннего и внешнего круга в случае квадрата? в случае треугольника?

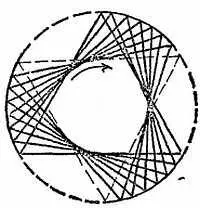
Фиг. 74. Те же две окружности, полученные вращением правильного многоугольника (в данном случае треугольника).

Вращение происходит вокруг центра, в плоскости треугольника. Вершины его будут лежать на внешней окружности, а стороны, скользя, образуют внутреннюю окружность.

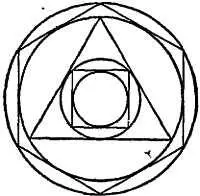
Фиг. 75. Окружности, образованные рядом правильных многоугольников, разделенных внутренними и внешними окружностями.

Окружности можно подобрать так, чтобы их размеры соответствовали соотношениям размеров орбит планет. Однако даже при самом удачном выборе многоугольников не удается получить модели Солнечной системы.

Однако такие построения оказывались неудовлетворительными, и однажды он воскликнул: «Почему фигуры, помогающие получить орбиты в пространстве , должны быть плоскими? Надо пользоваться объемными фигурами». Он знал, что существует всего пять правильных многогранников. Греческие математики доказали, что их может существовать не более пяти. Попытавшись осуществить с помощью пяти таких многогранников систему из шести сфер, Кеплер нашел, что этим сферам будет соответствовать шесть определенных орбит.

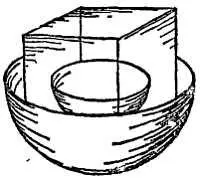
Фиг. 76. Вторая гипотеза Кеплера.

Этот рисунок иллюстрирует схему Кеплера, который пытался так расположить правильные многогранники, чтобы получить наилучшее согласие с известными соотношениями размеров орбит различных планет.

Правильные многогранники

Сколько может существовать различных правильных многогранников?

Правильный многогранник — это геометрическое тело с одинаковыми правильными плоскими гранями, т. е.

— все ребра имеют одинаковую длину

— все плоские углы одинаковы

— все пространственные углы одинаковы

— все грани имеют одну и ту же форму

(на фиг. 77, а даны примеры многогранников, не удовлетворяющих этим требованиям). Например, куб — правильный многогранник.

Фиг. 77. Многогранники.

а— неправильные

Грани правильного многогранника могут представлять собой:

— равносторонние треугольники

— квадраты

— правильные пятиугольники

и т. д.

Опыт 1. Доказательство для граней, представляющих собой квадраты .Попробуйте построить угол правильного многогранника из нескольких плоских прямых углов.