См. т. 1, стр. 75.
Волновое уравнение приводится к характерному виду
оно описывает любую волну, распространяющуюся со скоростью с . (Если вы знакомы с дифференциальным исчислением, попросите кого-нибудь из физиков показать вам этот замечательный раздел математической физики.) Это уравнение связывает распространение в пространстве со скоростью изменения во времени. Для величины, убывающей обратно пропорционально квадрату расстояния, 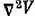 было бы нулем, а здесь оно равно величине, напоминающей ускорение. Для электромагнетизма величину d 2 V/d t 2можно связать с излучением волн при ускорении электронов. О смысле = 0 см. гл. 33 («(« Электростатика. Электрические заряды и поля », входит в т. 3 настоящего издания). Оно эквивалентно соотношению I в таблице на стр. 589, т. е. закону обратных квадратов.
было бы нулем, а здесь оно равно величине, напоминающей ускорение. Для электромагнетизма величину d 2 V/d t 2можно связать с излучением волн при ускорении электронов. О смысле = 0 см. гл. 33 («(« Электростатика. Электрические заряды и поля », входит в т. 3 настоящего издания). Оно эквивалентно соотношению I в таблице на стр. 589, т. е. закону обратных квадратов.
Для дополнения уравнения IV вам потребуется ввести постоянную K E, соответствующую К Hв уравнениях III. Знак минус в уравнении IV не необходим. Если уравнение IV дополнить, это несколько испортит симметрию, но этого требуют экспериментальные факты и сохранение энергии. Без этого не существовали бы радиоволны.
В нашем курсе используются другие обозначения (см. гл. 33 и 37 , т. 3). Силу между электрическими зарядами мы запишем в виде F= В∙( Q 1∙ Q 2)/ d 2. Сравнение с формулой Максвелла показывает, то наше В равно 1/ K E. Магнитную же силу между двумя отрезками проводов, по которым проходит ток, мы запишем в виде F= B'∙( C 1∙ L 1)∙( C 2∙ L 2)/ d 2, а наше В ' равно К H. Предсказание Максвелла v= 1/√( K E∙ K H) в. наших обозначениях выглядит так: v= √((1/ B)∙ B') = √( B'/ B). Измерив В и В ', можно предсказать скорость распространения электромагнитных волн. Арифметика здесь простая. Попытайтесь проделать вычисления и сравнить результат о измеренной скоростью света 3,0∙10 8м/сек. (В наших единицах B = 9,00∙10 9, a B '=10 -7.)
Гл. 37 (« Магнитные силы ») входит в т. 3 настоящего издания.
Хотя при движении по орбите скорость Земли меняется, мы считаем ее постоянной на протяжении короткого времени эксперимента. На самом деле постоянство будет точным, так как любое изменение скорости Земли полностью компенсируется силой гравитационного притяжения Солнца, вызывающего эти изменения. На Земле в целом (например, в ее центре) мы не можем заметить никакого эффекта и видим разностный эффект в разных точках Земли, например приливы. Собственное вращение Земли приводит к заметным эффектам; маятник Фуко изменяет плоскость своего качания, а ускорение g на экваторе и полюсе оказывается разным и т. п. Однако там, где эти различия существенны, их можно учесть.
Гл. 2 (« Полет снарядов. Геометрическое сложение: векторы ») входит в т. 1 настоящего издания.
Первое утверждение проще, ибо оно принадлежит наблюдателю, который запустил ракету в момент t = 0 из состояния покоя.
Например, он в момент t = 0 выпускает пулю, летящую со скоростью 1000 м/ceк в направлении оси X . Тогда попадание пули в мишень, отстоящую в 3 м, можно записать как х = 3 м, у = 0, z = 0, t = 0,003 сек.
Так древнегреческие философы называли универсальное вещество, которое, по их мнению, заполняет все пространство за пределами атмосферы.
Эта аберрация в корне отличается от параллакса — кажущегося движения ближайших звезд на фоне удаленных. Аберрация тоже заставляет звезды двигаться, но она относится ко всем звездам и на порядок больше параллакса даже ближайших звезд. (Кроме того, аберрация звезды пропорциональна скорости Земли и отстает по фазе на три месяца от ее параллакса.)
Это произошло задолго до успешных «земных» экспериментов (~1600): Галилей описал первую попытку определить время распространения вспышки сигнального фонаря между вершинами двух гор. Наблюдатель ε 1посылал вспышку наблюдателю ε 2, который, увидев ее, немедленно посылал сигнал ε 1. Пока ε 2не натренировался, они получали для света конечную скорость. Но по мере того как они совершенствовали свою технику, скорость вырастала все больше и больше, до,) «бесконечности» — скорость света слишком велика, чтобы можно было измерить ее таким способом.
Читать дальше

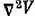 было бы нулем, а здесь оно равно величине, напоминающей ускорение. Для электромагнетизма величину d 2 V/d t 2можно связать с излучением волн при ускорении электронов. О смысле = 0 см. гл. 33 («(« Электростатика. Электрические заряды и поля », входит в т. 3 настоящего издания). Оно эквивалентно соотношению I в таблице на стр. 589, т. е. закону обратных квадратов.
было бы нулем, а здесь оно равно величине, напоминающей ускорение. Для электромагнетизма величину d 2 V/d t 2можно связать с излучением волн при ускорении электронов. О смысле = 0 см. гл. 33 («(« Электростатика. Электрические заряды и поля », входит в т. 3 настоящего издания). Оно эквивалентно соотношению I в таблице на стр. 589, т. е. закону обратных квадратов.






![Йэн Стюарт - Математика космоса [Как современная наука расшифровывает Вселенную]](/books/429584/jen-styuart-matematika-kosmosa-kak-sovremennaya-nau-thumb.webp)



