Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

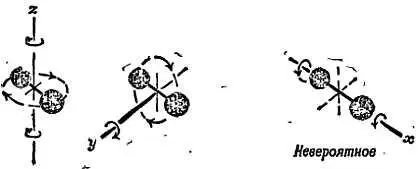
Фиг. 93. Вращательное движение.

Молекула из двух атомов (типа Н2) характеризуется двумя независимыми направлениями вращения. Здесь это вращения вокруг осей у и z .

У такой гантели, вообще говоря, имеются три независимые оси вращения. Однако вращение вокруг третьей оси (оси гантели) возбудить при соударениях слишком трудно. Таким образом, необходимо учитывать две доли вращательной энергии, кроме трех долей поступательной, каждая из которых равна 1/ 2 PV . Следовательно, при расчете теплоемкости водорода надо иметь в виду, что теплота расходуется на увеличение не только поступательной, но и вращательной энергии, т. е. вместо трех долей нужно учитывать пять. Его удельная теплоемкость поэтому должна быть в 5/ 3раза больше наших предсказаний, а 5/ 3∙(1,5) = 2,5; тогда согласие с экспериментальным результатом 2,40 оказывается очень хорошим. От этого же химики должны были бы прийти в восторг, ибо им не было известно, что такое молекула водорода: Н 2? Н 4? Н 6?…, теперь же они получили аргумент в пользу Н 2. К сожалению, все не так просто. Пара атомов в молекуле может еще колебаться друг относительно друга вдоль оси молекулы (фиг. 94).

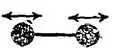
Фиг. 94. Колебательное движение вдоль оси молекулы.

Это движение обладает потенциальной и кинетической энергиями.

Колебательное движение потребует своей доли энергии, даже двойной доли, ибо любое колебание обладает как кинетической, так и потенциальной энергиями, а равномерное распределение обещает стандартную долю энергии каждой из них. Но тогда мы получили слишком много, 3,5. Экспериментальное значение теплоемкости водорода изменяется с температурой (фиг. 95).

Фиг. 95. Удельная теплоемкость водорода.

При очень низких температурах оно равно 1,5, в области комнатных температур 2,4, а при очень высоких — ползет к 3,5. Это как раз те значения теплоемкости, когда возбуждены такие движения:

Поступательное (3) (всего 3 доли)… удельная теплоемкость 1,5

Поступательное (3) + вращательное (2)… удельная теплоемкость 2,5

Поступательное (3) + вращательное (2) + колебательное (2)… удельная теплоемкость 3,5

Эти ступеньки для каждого из ожидаемых значений были загадкой, пока не сообразили, что они получаются из ограничений на вращательную и колебательную энергии — ограничений квантового типа. Квантовые правила возникшие из другого неожиданного поведения излучения, требуют, чтобы энергия на периодическое движение, такое, как колебания или вращение, бралась стандартными «порциями». Энергия каждой из таких «порций», или квантов, определяется правилом [217];

(ЭНЕРГИЯ КВАНТА) = (УНИВЕРСАЛЬНАЯ ПОСТОЯННАЯ)∙(ЧАСТОТА ПОВТОРЕНИЯ ДВИЖЕНИЯ)

Таким образом, вращение или колебание с высокой частотой должно обладать энергией в виде одной, двух, трех…. больших порций, возможно слишком больших, чтобы атом или молекула могли иметь хотя бы одну порцию для поддержания средней энергии, характерной для данной температуры. (Если бы сахар продавался и поедался только мешками по 100 кг, он исчез бы из рациона «среднего» жителя и лишь сказочным гигантам, пожалуй, такая норма была бы по вкусу.) Эти порционные ограничения на равномерное распределение энергии объясняют все особенности и предсказывают новые экспериментальные факты. Сообщим молекуле один квант энергии вращения. Это заставит ее вращаться очень быстро, ибо ее инерция вращения (момент инерции) довольно мала.

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩЕНИЯ = 1/ 2(МОМЕНТ ИНЕРЦИИ)∙(УГЛОВАЯ СКОРОСТЬ ВРАЩЕНИЯ) 2

Но при быстром вращении молекулы кванты ее энергии должны быть большими. Поэтому молекулы поглощают энергию либо большими квантами, либо не поглощают вовсе и не вращаются. При низких температурах средняя доля энергии, положенная по закону равномерного распределения, оказывается гораздо меньше одного кванта, так что вращаться могут лишь немногие молекулы. При комнатной температуре средняя доля составляет несколько квантов, и равномерное распределение осуществимо.

Молекулы колеблются с очень высокой частотой , поэтому практически ни одна из молекул не может колебаться, пока газ не нагрет до очень высокой температуры .

Удельная теплоемкость твердых тел