Любая обычная скорость настолько мала по сравнению с с , что отношение v / c будет очень мало, а v 2/ c 2— и того меньше. Следовательно, √(1 — ( v 2/ c 2)) практически равно единице. При малых скоростях масса оказывается постоянной, m= m 0/1.
Затем, приняв ньютоновское определение силы F= Δ( mv)/Δ tи измеряя работу произведением F ∙Δ s , Эйнштейн показал, что кинетическая энергия любого движущегося тела равна ( m — m 0)∙ с 2. Поскольку ( m — m 0) — это приращение массы вследствие движения, то E кин= ( приращение массы )∙ с 2. Это и есть соотношение Е= mc 2 для кинетической энергии и ее массы . Добавляя сюда постоянный запас энергии, заключенный в массе, m 0 с 2, Эйнштейн нашел, что
ПОЛНАЯ ЭНЕРГИЯ = ( m — m 0)∙ с 2+ m 0 с 2= mс 2.
(Более детально эти вопросы будут обсуждаться в гл. 31 , но даже там мы не дадим вывода, ибо он требует высшей математики.)
Формула E кин= ( m — m 0)∙ с 2выглядит совсем по-другому, чем E кин= 1/ 2 mv 2. Они действительно отличаются, как и должно быть. Но посмотрите на эту величину при малых скоростях. Предположим, что v мало по сравнению с с , так что и v 2/ c 2мало по сравнению с единицей. Затем, пользуясь теоремой о биноме (см. гл. 22 , примечание на стр. 239), получаем
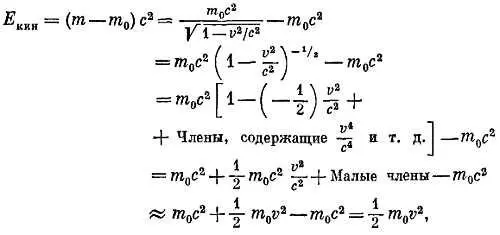
т. е. старое выражение для кинетической энергии. Вот как работает хорошая теория, воспроизводя в предельном случае старый результат и указывая на его ограничение — малые скорости.
Мы говорим, что дополнительная масса движущегося тела — это масса [174]его кинетической энергии. Тело с массой покоя т0 при любой скорости обладает массой m 0+ ( E кин/ c 2), как это нетрудно увидеть из вида кинетической энергии в теории относительности. При малых скоростях биномиальное приближение дает
m= m 0+ ( 1/ 2 mv 2/ c 2) = m 0 + E кин/ c 2.
На другом краю находится излучение, не имеющее массы покоя ( m 0 = 0). Это не вещество и его нельзя удержать в покое, оно просто имеет массу m и движется со скоростью с , так что его энергия равна mс 2. О порциях энергии, или квантах, мы говорим как о фотонах , когда хотим отметить поведение света как потока частиц. Каждый фотон имеет определенную массу m , определенную энергию Е= mc 2и количество движения (импульс) mс .
3) Ядерные превращения
В некоторых экспериментах с ядрами массы атомов после бурных взрывов, складываясь, не дают ту же самую полную массу. Освобожденная энергия уносит с собой и какую-то часть массы; кажется, что недостающая часть атомного материала исчезла. Однако если мы припишем измеренной энергии массу Е / с 2, то обнаружим, что масса сохраняется .
4) Аннигиляция вещества
Мы привыкли думать о массе как о неизбежном свойстве материи, поэтому переход массы из вещества в излучение — от лампы к улетающему лучу света — выглядит почти как уничтожение вещества . Еще один шаг — и мы с удивлением обнаружим то, что происходи: на самом деле положительный и отрицательный электроны, частички вещества, соединившись вместе, полностью превращаются в излучение. Масса их вещества превращается в равную ей массу излучения. Это случай исчезновения вещества в самом буквальном смысле. Как в фокусе, во вспышке света.
Измерения показывают, что ( энергия излучения при аннигиляции )/ с 2равна полной массе обоих электронов — положительного и отрицательного. Антипротон, соединяясь с протоном, аннигилирует, обычно с выбросом более легких частиц с большой кинетической энергией.
5) Создание вещества
Сейчас, когда мы научились распоряжаться высокоэнергетическим излучением (сверхкоротковолновыми рентгеновскими лучами), мы можем приготовить из излучения частицы вещества. Если такими лучами бомбардировать мишень, они дают иногда пару частиц, например положительный и отрицательный электроны. И если снова воспользоваться формулой m= Е/ с 2как для излучения, так и для кинетической энергии, то масса будет сохраняться.
Читать дальше

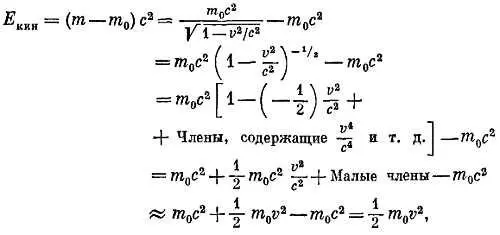







![Йэн Стюарт - Математика космоса [Как современная наука расшифровывает Вселенную]](/books/429584/jen-styuart-matematika-kosmosa-kak-sovremennaya-nau-thumb.webp)



