Нурбей Гулиа - Физика - Парадоксальная механика в вопросах и ответах

3.9. Вопрос. Если кориолисовы силы инерции нереальны, как они могут вызвать подмывание берегов рек? Что такое гироскопический эффект?

Ответ. Подмывание берегов рек можно качественно объяснить и без использования подвижной системы отсчета, эйлеровых сил инерции и других предположений.

Известно, что у рек, текущих в Северном полушарии, подмываются правые берега. Взглянем на Землю с высоты со стороны ее Северного полюса. Представим для простоты, что река, начинаясь на экваторе, течет прямо на север, пересекает Северный полюс и заканчивается тоже на экваторе, но уже с другой стороны. Вода в реке на экваторе имеет ту же скорость в направлении с запада на восток, как и ее берега (не течение реки, а именно скорость воды вместе с берегами и с Землей). Это при суточном вращении Земли составляет около 0,5 км/с. По мере приближения к полюсу скорость берегов уменьшается, а на самом полюсе она равна нулю. Но вода в реке «не хочет» уменьшать свою скорость – она подчиняется закону инерции. А скорость эта направлена в сторону вращения Земли – с запада на восток. Вот и начинает вода «давить» на восточный берег реки, который оказывается правым по течению. Дойдя до полюса, вода в реке полностью утратит свою скорость в «боковом» направлении, так как полюс – это неподвижная точка на Земле. Но река продолжает течь теперь уже на юг, и берега ее вращаются опять же с запада на восток со все увеличивающейся по мере приближения к экватору скоростью. Западный берег начинает «давить» на воду в реке, разгоняя ее с запада на восток, ну а вода, по третьему закону Ньютона, «давит» на этот берег, оказавшийся правым по течению.

На Южном полушарии все происходит наоборот. Если взглянуть на Землю со стороны Южного полюса, то вращается она уже в другом направлении. Все, у кого есть глобус, могут проверить это. Вот вам и закон Бэра, названный так в честь российского естествоиспытателя Карла Бэра (1792–1876), подметившего эту особенность рек.

А тут уже недалеко и до объяснения гироскопического эффекта вообще. Продолжим нашу реку дальше и опишем ею замкнутый круг на поверхности Земли. При этом заметим, что вся северная часть реки, находящаяся в Северном полушарии, будет стремиться направо, а вся южная часть – налево. Вот и все объяснение гироскопического эффекта, который считается едва ли не труднейшим в теоретической механике!

Итак, наша река – это огромное кольцо или маховик, вращающийся в том же направлении, что и течение реки. Если при этом поворачивать этот маховик в направлении вращения Земли, то вся северная его часть будет отклоняться вправо, а южная – влево (рис. 13). Иначе говоря, маховик будет поворачиваться так, чтобы его вращение совпало с направлением вращения Земли! Это и является качественным проявлением гироскопического эффекта.

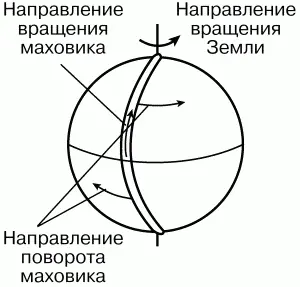
Рис. 13. Схема вращения маховика, «обернутого» вокруг Земли.

3.10. Вопрос. Говорят, что гироскопический эффект удерживает велосипед от падения. Так ли это?

Ответ. Приходится много читать о том, что устойчивость велосипеда достигается благодаря гироскопическому эффекту его колес. Между тем – это явное преувеличение, и вот почему.

Гироскопический эффект – это возникновение момента при попытке принудительного поворота оси вращающегося тела. Но величину гироскопического момента мы пока не определяли. При поворачивании оси велосипедного колеса этот момент равен произведению момента инерции колеса на угловые скорости его вращения и поворота оси (вынужденной прецессии). Для простоты решим, что масса колеса 2 кг, радиус его 0,25 м и, стало быть, момент инерции, примерно равный произведению массы на квадрат радиуса, равен 0,125 кг?м2. Велосипедист спокойно маневрирует уже на скорости 1 м/с, и колесо при этом вращается с угловой скоростью 4 рад/с. Угловая скорость поворота оси колеса раз в 20 меньше и равна примерно 0,2 рад/с. В результате получаем гироскопический момент, равный 0,1 Н?м. Это то же самое, что гирьку в 1 кг подвесить на конец гвоздя, торчащего из стены всего на 1 см. Вряд ли такой ничтожный момент может что-либо изменить в движении велосипеда.

В то же время едущий велосипедист, свернув всего на 10 см от прямой, если не наклонится в сторону поворота, создаст опрокидывающий момент, равный его весу плюс примерно полвеса велосипеда, умноженные на 0,1 м, что достигает порядка 100 Н?м. Этот момент в тысячу раз больше, чем гироскопический момент! Вот таким образом, наклоняясь к центру поворота, велосипедист сохраняет устойчивость.