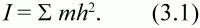Нурбей Гулиа - Физика - Парадоксальная механика в вопросах и ответах

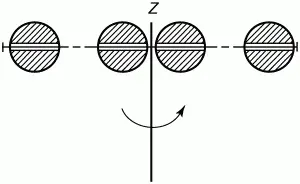
Рис. 6. Схема изменения момента инерции тела.

Стало быть, инертность тела при вращении зависит не только от массы, но в большей степени от распределения этой массы относительно оси вращения. Мерой инертности тела при вращении является осевой момент инерции I , равный сумме произведений масс т всех частиц тела на квадраты их расстояний h от оси вращения:

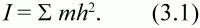
Осевой момент инерции играет при вращательном движении ту же роль, что и масса при поступательном (прямолинейном), и таким образом, он является мерой инертности (инерции) тела при вращательном движении.

Как мы знаем, закон инерции устанавливает эквивалентность относительного покоя и равномерного прямолинейного движения – движения по инерции. Нельзя никаким механическим опытом определить, покоится ли данное тело или движется равномерно и прямолинейно. Во вращательном движении это не так. Например, совсем не безразлично, покоится ли волчок, или вращается равномерно с постоянной угловой скоростью. Как отмечал А. Ю. Ишлинский [17], угловая скорость твердого тела является величиной, характеризующей его физическое состояние. Угловую скорость можно измерить, например, с помощью определения упругих деформаций тела, без какой-либо информации о положении тела по отношению к «абсолютной» системе координат. Поэтому термин «абсолютная угловая скорость тела» в отличие от «абсолютной скорости точки» должен употребляться в прямом смысле (без кавычек).

Таким образом, механические явления в покоящейся и вращающейся системах будут протекать по-разному, не говоря уже о том, что если тело достаточно сильно раскрутить, то его разорвет на части из-за возникших в нем напряжений.

Еще одно отличие состоит в том, что прямолинейное равномерное движение и покой эквивалентны, а вращение, даже с постоянной угловой скоростью, может быть четко отграничено не только от покоя, но и от вращения с другой угловой скоростью.

Здесь уместно упомянуть о взглядах австрийского физика Эрнста Маха (1838–1916), оказавшего большое влияние на формирование принципа эквивалентности Эйнштейна. Мах «подбором» соответствующей системы координат стремился придать законам механики такой вид, чтобы они не зависели от вращения. Что получилось бы, если бы ему это удалось? Давайте поместим быстро вращающегося наблюдателя на неподвижный маховик. Тогда можно сказать, что относительно наблюдателя маховик быстро вращается, может, даже быстрее, чем позволяет его прочность. Но маховик не разорвется, хотя наблюдателю кажется, что на него действуют огромные напряжения. А сам вращающийся наблюдатель может пострадать, так как при вращении именно в нем возникают механические напряжения.

3.2. Вопрос. Можно ли сформулировать законы инерции вращения аналогично первому закону Ньютона?

Ответ. Можно взять на себя смелость по образу и подобию первого закона Ньютона сформулировать «закон» инерции вращательного движения: «Изолированное от внешних моментов абсолютно твердое тело будет сохранять состояние покоя или равномерного вращения вокруг неподвижной оси до тех пор, пока приложенные к этому телу внешние моменты не заставят его изменить это состояние».

Почему же абсолютно твердое тело, а не любое? Потому, что у нетвердого тела из-за вынужденных деформаций при вращении изменится момент инерции, а это равносильно изменению массы точки для первого закона Ньютона.

В случае вращательного движения, если момент инерции непостоянен, придется принять за константу не угловую скорость, а произведение угловой скорости ю на момент инерции /– так называемый кинетический момент К. В этом случае «закон» инерции вращения примет более общую форму: «Изолированное от внешних моментов тело будет сохранять вектор своего кинетического момента постоянным». Если же тело вращается вокруг неподвижной оси: «Изолированное от внешних моментов относительно оси вращения тело будет сохранять кинетический момент относительно этой оси постоянным». Эти законы, правда, в несколько иной формулировке, называются законами сохранения кинетического момента.

3.3. Вопрос. Земля и Луна вращаются вокруг общего центра масс. Действуют ли на эти небесные тела центробежные силы?