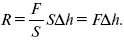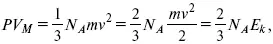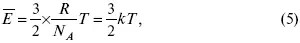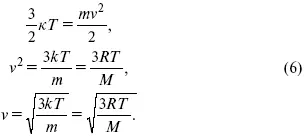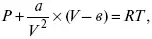А. Березовчук - Физическая химия - конспект лекций

R = P Δ V

Поскольку P = F / S , а Δ V равно площади сосуда S , умноженной на высоту подъема его поршня Δ h , имеем

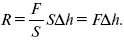
Очевидно, что справа получим выражение для работы, и это подтверждает физический смысл газовой постоянной.

Очень плодотворным в середине XIX века оказалось представление о молекулярном строении вещества. Когда была принята гипотеза А. Авогадро о том, что в киломоле любого вещества содержится одно и то же количество структурных единиц: 6,02 x 10 26кмоля = 6,02 x 10 23моля, поскольку молярная масса воды M(H 2O) = 18 кг/кмоль , следовательно, в 18 литрах воды находится столько же молекул, сколько в 22,4 м 3водяного пара. Это позволяет легко понять, что расстояние между молекулами газообразной воды (пара) значительно больше, в среднем на один порядок, чем в жидкой воде. Можно предположить, что это выполняется для любого вещества. Считая, что в газах молекулы движутся хаотически, можно вывести так называемое основное уравнение кинетической теории:

где Na – 6,02 x 10 26кмоль = 6,02 x 10 23моль – число Авогадро;

V M – молекулярный объем = 22,4 м 3;

m – масса одной молекулы;

v – скорость молекулы.

Преобразуем уравнение (4):

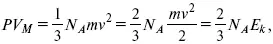
где E k – энергия одной молекулы.

Видно, что справа стоит полная кинетическая энергия всех молекул. С другой стороны, сравнивая с уравнением Менделеева – Клапейрона, видим, что это произведение равно RT.

Это позволяет выразить среднюю кинетическую энергию молекулы газа:

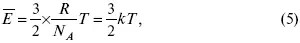
где к = R / Na – постоянная Больцмана, равная 1,38 ґ 10– 23кДж/кмоль. Зная кинетическую энергию молекулы, можно рассчитать ее среднюю скорость

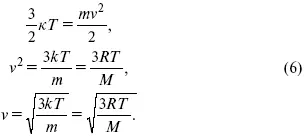
Около 1860 г. Д. К. Максвелл вывел функцию, описывающую распределение молекул газа по скоростям. Эта функция имеет на графике вид характерной кривой с максимумом около наиболее вероятной скорости примерно 500 м/с. Важно заметить, что существуют молекулы со скоростями, превышающими этот максимум. С другой стороны, уравнение (6) позволяет сделать вывод об увеличении доли молекул с большими скоростями при нагревании газа. Спустя почти 60 лет гениальная догадка Д. К. Максвелла была подтверждена в опытах О. Штерна .

Исследования показали, что уравнение Менделеева – Клапейрона не очень точно выполняется при исследовании разных газов. Голландский физик Я. Д. Ван-дер-Ваальс первым понял причины этих отклонений: одна из них состоит в том, что вследствие огромного числа молекул, их собственный объем в целом сравним с объемом сосуда, в котором находится газ. С другой стороны, существование взаимодействия между молекулами газа слегка искажает показание манометров, с помощью которых обычно измеряют давление газа. В итоге Ван-дер-Ваальс получил уравнение следующего вида:

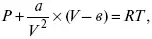
где а , в – постоянные величины для различных газов.

Недостаток этого уравнения в том, что а и в должны быть измерены для каждого газа эмпирически. Преимущество в том, что оно включает область перехода газа в жидкую фазу при высоких давлениях и низких температурах. Осознание этого сделало возможным получать любой газ в жидкой фазе.

Химическая термодинамика– наука, изучающая условия устойчивости систем и законы.

Термодинамика– наука о макросистемах.

Она позволяет apriori определить принципиальную невозможность того или иного процесса. Физические и химические явления в термодинамике исследуются с помощью основных законов термодинамики. Состояние рассматриваемых объектов в термодинамике определяется непосредственно измеряемыми величинами, характеризующими вещества; механизм процесса и сама структура вещества не рассматриваются.