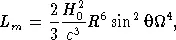 |
(22.2) |
где 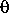 — угол между магнитной осью и осью вращения, H 0 — напряженность магнитного поля на поверхности пульсара. Например, пульсар в Крабовидной туманности NP 0531, для которого
— угол между магнитной осью и осью вращения, H 0 — напряженность магнитного поля на поверхности пульсара. Например, пульсар в Крабовидной туманности NP 0531, для которого  = 200 с -1,
= 200 с -1, 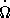 = 2 , 4
= 2 , 4  10 -9, теряет энергию
10 -9, теряет энергию 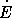 = 3
= 3  10 38эрг/с. Если причина торможения — магнитно-дипольное излучение, то, приравнивая
10 38эрг/с. Если причина торможения — магнитно-дипольное излучение, то, приравнивая 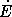 = L m , найдем, что H 0
= L m , найдем, что H 0  3
3  10 12Э. Другой причиной торможения этого пульсара может быть излучение им гравитационных волн (см. § 24). Для этого надо только предположить, что фигура нейтронной звезды слегка асимметрична, т. е. представляет собой трехосный эллипсоид. В этом случае мощность гравитационного излучения вращающейся нейтронной звезды определяется формулой
10 12Э. Другой причиной торможения этого пульсара может быть излучение им гравитационных волн (см. § 24). Для этого надо только предположить, что фигура нейтронной звезды слегка асимметрична, т. е. представляет собой трехосный эллипсоид. В этом случае мощность гравитационного излучения вращающейся нейтронной звезды определяется формулой
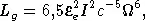 |
(22.3) |
где I — момент инерции, а 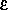 e — эксцентриситет экваториального эллипса нейтронной звезды. Частота гравитационных волн, как оказывается, равна удвоенной частоте вращения.
e — эксцентриситет экваториального эллипса нейтронной звезды. Частота гравитационных волн, как оказывается, равна удвоенной частоте вращения.
Как видно из этой формулы, зависимость мощности гравитационного излучения от угловой скорости  значительно более сильная, чем в случае магнитно-дипольного излучения. Поэтому заметный эффект может быть только у очень быстро вращающихся пульсаров, например, у NP 0531 (см. об этом в § 24). В том случае, когда центр магнитного диполя не совпадает с центром нейтронной звезды, излучение будет асимметричным. В этом случае звезда приобретет импульс отдачи в направлении от вращения. Не этим ли объясняются высокие скорости пульсаров?
значительно более сильная, чем в случае магнитно-дипольного излучения. Поэтому заметный эффект может быть только у очень быстро вращающихся пульсаров, например, у NP 0531 (см. об этом в § 24). В том случае, когда центр магнитного диполя не совпадает с центром нейтронной звезды, излучение будет асимметричным. В этом случае звезда приобретет импульс отдачи в направлении от вращения. Не этим ли объясняются высокие скорости пульсаров?
Если бы торможение вращающихся нейтронных звезд было обусловлено их магнитно-дипольным излучением, то, как можно показать, 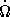
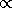
 3. Между тем статистический анализ большого количества пульсаров с известными
3. Между тем статистический анализ большого количества пульсаров с известными  и
и 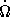 дает эмпирическую зависимость
дает эмпирическую зависимость 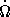
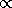
 3 , 4. У пульсара NP 0531, для которого
3 , 4. У пульсара NP 0531, для которого  и
и 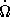 наблюдались особенно тщательно, эмпирическая зависимость имеет вид
наблюдались особенно тщательно, эмпирическая зависимость имеет вид 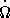
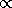
 2 , 7. Это означает, что рассмотренная выше простая модель торможения намагниченных вращающихся нейтронных звезд недостаточна. И прежде всего предположение, что нейтронная звезда находится в вакууме, заведомо не выполняется. Тем самым задача становится значительно более сложной.
2 , 7. Это означает, что рассмотренная выше простая модель торможения намагниченных вращающихся нейтронных звезд недостаточна. И прежде всего предположение, что нейтронная звезда находится в вакууме, заведомо не выполняется. Тем самым задача становится значительно более сложной.
Вращающийся намагниченный проводник создает в окружающем пространстве электрическое поле. Составляющая этого поля, перпендикулярная к поверхности проводника, будет стремиться «вырвать» из него электроны и ионы. В реальных условиях нейтронной звезды напряженность электрического поля достигает огромных значений. К тому же температура поверхности нейтронной звезды достаточно высока. По этим причинам пространство вокруг нейтронной звезды заполнится большим количеством заряженных частиц, которые, двигаясь по силовым линиям магнитного поля, будут вместе с нейтронной звездой с той же угловой скоростью вращаться вокруг ее оси. Такое «твердотельное» вращение должно иметь место вплоть до некоторого критического расстояния от оси вращения, т. е. внутри цилиндра. Радиус этого цилиндра R 1= c/  определяется условием, что на его поверхности скорость твердотельного вращения равна скорости света
определяется условием, что на его поверхности скорость твердотельного вращения равна скорости света [ 54 ] По этой причине указанный цилиндр называется «световым цилиндром».
. Однако если плотность плазмы вокруг нейтронной звезды достаточно велика, область ее твердотельного вращения будет меньше и определится условием равенства плотностей магнитной энергии и кинетической энергии плазмы.
Читать дальше

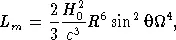
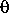 — угол между магнитной осью и осью вращения, H 0 — напряженность магнитного поля на поверхности пульсара. Например, пульсар в Крабовидной туманности NP 0531, для которого
— угол между магнитной осью и осью вращения, H 0 — напряженность магнитного поля на поверхности пульсара. Например, пульсар в Крабовидной туманности NP 0531, для которого  = 200 с -1,
= 200 с -1, 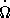 = 2 , 4
= 2 , 4  10 -9, теряет энергию
10 -9, теряет энергию 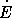 = 3
= 3  10 38эрг/с. Если причина торможения — магнитно-дипольное излучение, то, приравнивая
10 38эрг/с. Если причина торможения — магнитно-дипольное излучение, то, приравнивая 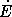 = L m , найдем, что H 0
= L m , найдем, что H 0  3
3  10 12Э. Другой причиной торможения этого пульсара может быть излучение им гравитационных волн (см. § 24). Для этого надо только предположить, что фигура нейтронной звезды слегка асимметрична, т. е. представляет собой трехосный эллипсоид. В этом случае мощность гравитационного излучения вращающейся нейтронной звезды определяется формулой
10 12Э. Другой причиной торможения этого пульсара может быть излучение им гравитационных волн (см. § 24). Для этого надо только предположить, что фигура нейтронной звезды слегка асимметрична, т. е. представляет собой трехосный эллипсоид. В этом случае мощность гравитационного излучения вращающейся нейтронной звезды определяется формулой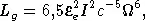
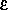 e — эксцентриситет экваториального эллипса нейтронной звезды. Частота гравитационных волн, как оказывается, равна удвоенной частоте вращения.
e — эксцентриситет экваториального эллипса нейтронной звезды. Частота гравитационных волн, как оказывается, равна удвоенной частоте вращения. значительно более сильная, чем в случае магнитно-дипольного излучения. Поэтому заметный эффект может быть только у очень быстро вращающихся пульсаров, например, у NP 0531 (см. об этом в § 24). В том случае, когда центр магнитного диполя не совпадает с центром нейтронной звезды, излучение будет асимметричным. В этом случае звезда приобретет импульс отдачи в направлении от вращения. Не этим ли объясняются высокие скорости пульсаров?
значительно более сильная, чем в случае магнитно-дипольного излучения. Поэтому заметный эффект может быть только у очень быстро вращающихся пульсаров, например, у NP 0531 (см. об этом в § 24). В том случае, когда центр магнитного диполя не совпадает с центром нейтронной звезды, излучение будет асимметричным. В этом случае звезда приобретет импульс отдачи в направлении от вращения. Не этим ли объясняются высокие скорости пульсаров?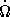
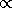
 3. Между тем статистический анализ большого количества пульсаров с известными
3. Между тем статистический анализ большого количества пульсаров с известными  и
и 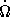 дает эмпирическую зависимость
дает эмпирическую зависимость 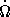
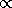
 3 , 4. У пульсара NP 0531, для которого
3 , 4. У пульсара NP 0531, для которого  и
и 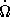 наблюдались особенно тщательно, эмпирическая зависимость имеет вид
наблюдались особенно тщательно, эмпирическая зависимость имеет вид 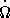
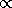
 2 , 7. Это означает, что рассмотренная выше простая модель торможения намагниченных вращающихся нейтронных звезд недостаточна. И прежде всего предположение, что нейтронная звезда находится в вакууме, заведомо не выполняется. Тем самым задача становится значительно более сложной.
2 , 7. Это означает, что рассмотренная выше простая модель торможения намагниченных вращающихся нейтронных звезд недостаточна. И прежде всего предположение, что нейтронная звезда находится в вакууме, заведомо не выполняется. Тем самым задача становится значительно более сложной. определяется условием, что на его поверхности скорость твердотельного вращения равна скорости света
определяется условием, что на его поверхности скорость твердотельного вращения равна скорости света 




![Андрэ Нортон - Рожденные среди звезд [= Рождение звезды]](/books/322400/andre-norton-rozhdennye-sredi-zvezd-rozhdenie-zve-thumb.webp)
![Эдвард Радзинский - Тираны России и СССР [Распутин. Жизнь и смерть + Сталин. Жизнь и смерть]](/books/391099/edvard-radzinskij-tirany-rossii-i-sssr-rasputin-thumb.webp)


