Роджер Пенроуз - Большое, малое и человеческий разум

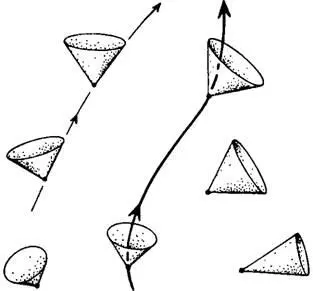
Специальная теория относительности во многих отношениях не только значительно проще классической механики, но и выглядит гораздо изящнее с математической точки зрения (в частности, при рассмотрении процессов в рамках теории групп). В специальной теории относительности пространство-время является плоским, а все световые конусы выстраиваются вдоль траекторий, как было показано на рис. 1.8. При переходе к более сложной общей теории относительности (теории пространства-времени с учетом гравитации) ясная физическая картина на первый взгляд «мутнеет» и теряет свою простоту, так как световые конусы оказываются разбросанными по всему пространству (рис. 1.11). Ранее я говорил, что, развивая любую теорию все глубже и глубже, мы должны приходить к более простым математическим выражениям. Представленная мною картина пока выглядит ужасающе сложной, однако если мы проявим немного терпения, то убедимся, что математическая простота и изящество теории возникнут снова.

Рис. 1.11. Искривленное пространство-время.

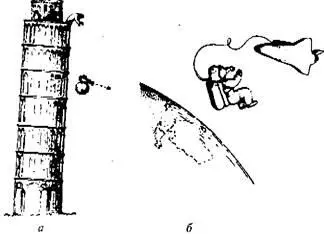
Напомню вам основные положения эйнштейновской теории тяготения. Прежде всего, она основана на принципе эквивалентности Галилея. На рис. 1.12 я попытался изобразить Галилея, бросающего с вершины знаменитой Пизанской башни большой и маленький камни. Независимо от того, действительно ли Галилей проводил такие эксперименты, он совершенно ясно установил, понял и сформулировал правило, что оба камня долетят до поверхности Земли за одинаковое время, если не учитывать сопротивления воздуха при падении. Если бы вы находились на одном из этих камней, то второй казался бы вам неподвижно висящим в воздухе (для более наглядной демонстрации этого факта я пририсовал телекамеру к одному из камней). В наше время эффект свободного парения очень часто демонстрируют при репортажах с космических кораблей, и недавно я сам видел британского космонавта, свободно «плавающего» в пространстве рядом с огромным космическим аппаратом (полная аналогия с большим и маленьким камнями в опытах Галилея). Именно это явление и называют принципом эквивалентности.

Рис. 1.12.

а— Галилей бросает с наклонной Пизанской башни два камня (один с телекамерой); б— астронавт и космический корабль, плавающие в пространстве как бы без воздействия гравитации.

Рассматривая гравитацию в рамках опытов со свободным падением, мы вдруг понимаем, что в этих условиях она как бы полностью исчезает. Однако эйнштейновская теория вовсе не утверждает , что тяготение исчезает , она всего лишь говорит об исчезновении силы тяжести , что означает совершенно иное явление, которое можно назвать «приливным эффектом» гравитации.

Для дальнейшего изложения мне необходимо ввести еще несколько математических понятий. Мы говорим об искривлении пространства-времени, а процессы такого типа описываются тензором , который я для удобства назову Риманоми буду обозначать заглавной буквой Rв простом уравнении, которое выпишу чуть ниже. Я не буду объяснять вам, в чем состоит физический смысл тензора кривизны Римана, обозначенного R, а только отмечу, что тензоры имеют некоторое число нижних индексов, вместо которых в уравнение поставлено соответствующее число точек (внизу справа от знака тензора). Тензор кривизны R можно разложить на две составляющие (одну из которых я назову кривизной Вейля, а вторую — кривизной Риччи), что позволяет мне выписать уравнение

Риман = Вейль + Риччи

R.... = C... +R'...g..,

где формально величины Си R'являются тензорами кривизны Вейля и Риччи, a g— так называемый метрический тензор.

Кривизна Вейля является объективным показателем упомянутого выше «приливного эффекта», физическую природу которого я поясню сейчас на простом примере. С точки зрения космонавта гравитация исчезает, однако мы понимаем, что это не так. Представьте себе, например, что космонавт окружен сферическим облаком неподвижных относительно него частиц. С течением времени это облако начнет «расплываться» и деформироваться, после чего в результате очень небольшого различия сил тяготения в различных участках сферы (мне хочется особо подчеркнуть, что я могу вполне адекватно описать эффект в рамках ньютоновской механики) сферическое облако через некоторое время превратится в эллипсоид, как показано на рис. 1.13, а .