Роджер Пенроуз - Большое, малое и человеческий разум

Рис. 1.13.

а— приливный эффект. Широкие стрелки показывают направление относительного ускорения частиц; б— если сферическое облако окружает какой-либо массивный объект (например, Землю), то оно испытывает в целом ускорение, направленное «внутрь».

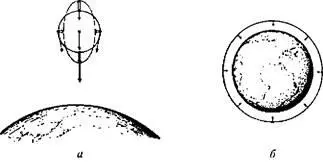
Как я уже говорил, искажение отчасти объясняется тем, что частицы, расположенные ближе к Земле, ускоряются сильнее, чем частицы на периферии облака. Кроме того, частицы по «бокам» сферы испытывают небольшие ускорения «внутрь», что также показано на рис. 1.13, а . Обе эти причины способствуют образованию эллипсоида из первоначально сферического облака частиц. Описываемый эффект очень удачно был назван «приливным», поскольку достаточно заменить Землю в наших рассуждениях Луной, а облако частиц — мировым океаном, как мы сразу поймем, почему поверхность морей на нашей планете не представляет собой правильную сферу! В соответствии с совершенно таким же механизмом морская толща на обращенной к Луне поверхности Земли притягивается Луной чуть сильнее, чем на обратной стороне, в результате чего вдоль морской поверхности дважды в день пробегает высокая приливная водна.

Гравитационный эффект по Эйнштейну представляет собой просто другую форму описанного приливного эффекта. Он определяется, как уже отмечалось, кривизной Вейля , т. е. составляющей С...выписанного выше уравнения. Эта часть тензора кривизны соответствует процессам с «сохранением объема» (т. е. объем эллипсоида, образовавшегося в результате деформации сферы из частиц, должен в точности равняться объему исходной сферы).

Вторая составляющая, называемая кривизной Риччи , относится к эффектам, связанным с «сокращением объема». Например, если Земля будет окружена сферическим облаком частиц (как показано на рис. 1.13, б ), то объем сферы с течением времени должен несколько уменьшиться, поскольку все частицы притягиваются «внутрь». Степень такого сокращения объема и описывается составляющей R'. В соответствии с эйнштейновской теорией эта кривизна определяется количеством вещества в ближайшем окружении данной точки. Иными словами, определив правильным образом плотность вещества в некоторой точке пространства, мы можем найти и величину направленного «внутрь» ускорения. При таком подходе теория Эйнштейна полностью совпадает с ньютоновской теорией тяготения.

Именно так Эйнштейн и сформулировал свою теорию гравитации — он выразил тяготение посредством приливных эффектов, являющихся мерой локального искривления пространства-времени. Представление об искривлении четырехмерного пространства-времени является важнейшим в теории относительности. Я напомню вам рис. 1.11, где схематически были показаны мировые линии частиц и их искажения. Теория Эйнштейна представляет собой чисто геометрическую схему для четырехмерного пространства-времени, причем ее математическая формулировка отличается удивительной красотой.

История открытия общей теории относительности является весьма поучительной и интересной. Эйнштейн полностью сформулировал ее в 1915 г., исходя не из экспериментальных наблюдений, а лишь из некоторых эстетических, геометрических и физических принципов и пристрастий. Основой теории стали принцип эквивалентности Галилея (примером действия которого могут служить описанные выше эксперименты с бросанием камней различного веса, рис. 1.12) и общие идеи неевклидовой геометрии, естественным образом используемые для описания пространства-времени. Об экспериментальных доказательствах теории вначале никто не задумывался, однако после ее окончательной формулировки было предложено три разных варианта проверки. Первый из них связан с известной астрономической задачей (проблема смещения перигелия Меркурия), которую никак не удавалось решить в рамках классической механики Ньютона. Общая теория относительности позволила совершенно точно предсказать величину этого смещения. Далее, из теории следовало, что траектория световых лучей должна искривляться при прохождении через мощные гравитационные поля (например, вблизи Солнца). Для проверки этой гипотезы в 1919 г. под руководством Артура Эддингтона была организована астрономическая экспедиция для наблюдения полного солнечного затмения. Результаты, полученные этой знаменитой экспедицией, соответствовали предсказаниям эйнштейновской теории (рис. 1.14, а ). И наконец, третья проверка была связана с предсказанием замедления хода часов в гравитационном поле (часы у поверхности Земли должны идти чуть медленнее, чем часы на вершине башни), что неоднократно проверялось в экспериментах. Следует отметить, что все эти проверки не оказались достаточно вескими (из-за того, что наблюдаемые эффекты всегда очень слабы), а также могут быть достаточно убедительно объяснены в рамках других теорий.