Роджер Пенроуз - Большое, малое и человеческий разум

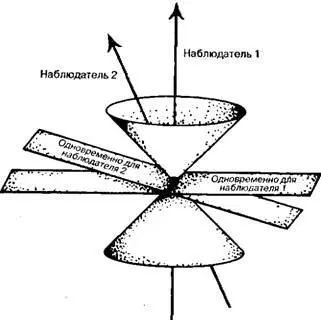
Рис. 1.9. Относительность понятия одновременности в специальной теории относительности Эйнштейна.

Наблюдатели 1 и 2 движутся в пространстве-времени относительно друг друга, в результате чего события, одновременные для наблюдателя 1, перестают быть одновременными для наблюдателя 2, и наоборот.

Мы можем придать группе Лоренца и несколько иную трактовку. Как уже подчеркивалось, световой конус является одной из важнейших структур пространства-времени. Представьте себя наблюдателем, рассматривающим Вселенную из какой-то точки пространства. В ваши глаза попадает свет от далеких звезд, и в соответствии с концепцией пространства-времени наблюдаемые вами события представляют собой пересечения мировых линий звезд с вашим световым конусом прошлого, как это показано на рис. 1.10. Другими словами, в вашем световом конусе прошлого звезды в некоторый момент времени образуют некий рисунок на небесной сфере (рис. 1.10, а ). Предположим, что второй наблюдатель, двигаясь с большой скоростью относительно вас, именно в этот момент оказывается рядом. Он воспринимает те же звезды, однако ему кажется, что они занимают на сфере другие положения (рис. 1.10, б ) — этот эффект астрономы называют аберрацией . Существует набор преобразований, позволяющий связать друг с другом изображения, воспринимаемые различными наблюдателями. В каждом из таких преобразований сфера соотносится с другой сферой, однако среди этих преобразований есть специальное, в котором точным окружностям соответствуют точные окружности, в результате чего при преобразовании сохраняются значения углов, т. е. воспринимаемые вами круглые изображения остаются круглыми и для другого наблюдателя.

Рис. 1.10. Картина звездного неба для двух различных наблюдателей,

а— наблюдатели 1 и 2 из одной и той же точки рассматривают звезды в световом конусе прошлого. Места пересечения светового конуса со звездами указаны черными точками. Световые сигналы идут от звезд к наблюдателям вдоль светового конуса. Наблюдатель 2 движется в пространстве-времени относительно наблюдателя 1 с некоторой скоростью; б— расположение звезд на небе, как его видят наблюдатели 1 и 2, когда они оказываются в одной точке пространства-времени; в— наглядное представление преобразования картины звездного неба для различных наблюдателей при использовании стереографической проекции (окружности переходят в окружности, значения углов сохраняются).

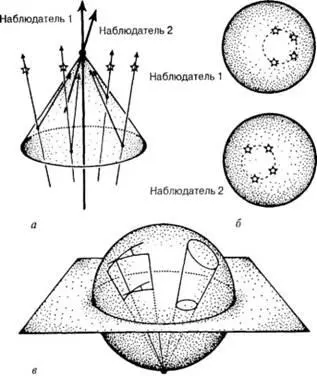
Существует прекрасная иллюстрация механизма действия таких преобразований, которая, кстати, одновременно демонстрирует исключительную элегантность и красоту математической физики при описании фундаментальных понятий и представлений. На рис. 1.10, в показана сфера, пересекаемая плоскостью по экватору. Мы можем нарисовать на поверхности этой сферы различные фигуры, а затем рассмотреть их так называемые стереографические проекции (проекции из южного полюса сферы на экваториальную плоскость), обладающие довольно необычными свойствами. Действительно, как видно из рисунка, при такой проекции не только окружности на сфере превращаются в окружности на плоскости, но сохраняются и точные значения всех углов, образуемых пересечением кривых на сфере. В гл. 2 я более подробно расскажу об этом типе проекций (см. рис. 2.4) и покажу, что с его помощью можно сопоставить все точки сферы комплексным числам (такие числа возникают при извлечении квадратного корня из отрицательных чисел), а затем перевести в точки экваториальной плоскости. Такая операция, в которую можно вовлечь все множество комплексных чисел (включая «бесконечные» значения), позволяет построить структуру, называемую сферой Римана .

Для читателя, заинтересовавшегося этой проблемой, я приведу формулу

u -> u' = (αu + ß) / (γu + δ) ,

описывающую преобразование (аберрации) Лоренца, которое переводит окружности в окружности и одновременно сохраняет значения всех углов. Преобразования такого типа называют преобразованиями Мёбиуса. Мне бы хотелось лишь отметить простоту и изящество этой формулы, описывающей столь сложный параметр, каким выступает в данной ситуации величина и . Совершенно удивительным кажется то, что при указанных преобразованиях в специальной теории относительности конечная формула имеет очень простой вид, в то время как соответствующие преобразования аберрации в ньютоновской механике описываются очень сложными выражениями. Как это часто бывает в физике, переход к более фундаментальным понятиям и более точным теориям приводит к упрощению математического описания, хотя на первый взгляд такой переход должен сопровождаться усложнением формального аппарата. Примером этой важной закономерности может служить разительный контраст между понятиями относительности в механике Галилея и Эйнштейна.