Лекции по схемотехнике

- Последовательное суммирование;

- Параллельное суммирование с последовательным переносом;

- Параллельное суммирование с параллельным переносом.

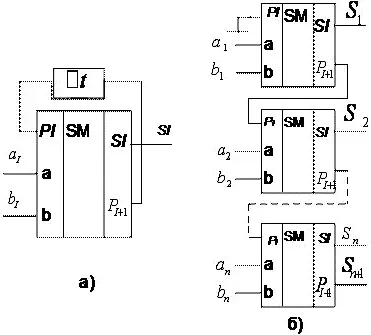
Рисунок 24 Суммирование многоразрядных чисел: а) — Последовательное; б) — Параллельное с последовательным переносом

При последовательном суммировании используется один сумматор, общий для всех разрядов (Рисунок 24, а). Операнды должны вводиться в сумматор через входы а I и b I синхронно, начиная с младших разрядов. Цепь задержки обеспечивает хранение импульса переноса P I +1на время одного такта, то есть до прихода пары слагаемых следующего разряда, с которыми он будет просуммирован. Задержку выполняет D-триггер. Результаты суммирования также считываются последовательно, начиная с младших разрядов. Для хранения и ввода операндов на входы сумматора, а также для записи результата суммирования обычно используются регистры сдвига.

Достоинство этого метода — малые аппаратные затраты.

Недостаток — невысокое быстродействие, так как одновременно суммируются только пара слагаемых.

Схема параллельного сумматора с последовательным переносом приведена на рисунке 24, б). Количество сумматоров равно числу разрядов чисел. Выход переноса P I +1каждого сумматора соединяется со входом переноса P I следующего более старшего разряда. На входе переноса младшего разряда устанавливается потенциал «0», так как сигнал переноса сюда не поступает. Слагаемые a I и b I суммируются во всех разрядах одновременно, а перенос P I поступает с окончанием операции сложения в предыдущем разряде.

Быстродействие таких сумматоров ограничено задержкой переноса, так как формирование переноса на выходе старшего разряда не может произойти до тех пор, пока сигнал переноса не распространится по всей цепочке сумматоров.

Для организации параллельного переноса применяются специальные узлы — блоки ускоренного переноса.

Принцип ускоренного переноса заключается в том, что для каждого двоичного разряда дополнительно находятся два сигнала:

G — образование переноса и H — распространение переноса.

G I= a I·b I

H I= a I+ b I

В случае G I =1, то есть a I=b I =1, в данном i-разряде формируется сигнал переноса P I +1в следующий высший разряд независимо от формирования функций суммы в предыдущих разрядах.

Если хотя бы одно из слагаемых a I или b I равно «1», то есть H I =1, то перенос в последующий разряд производится при наличии сигнала переноса из предыдущего разряда.

Если H I=H I –1=1 и при этом существует сигнал переноса P I из предыдущего в i-й разряд, то перенос производится сразу в i+2 разряд.

В общем случае процесс формирования ускоренного переноса описывается следующим уравнением:

P I +1= G I+ H I · G I –1+ H I · H I –1· G I –2+ … + H I · H I –1·…· H 2· H 1· P 1

Блоки ускоренного переноса выпускаются в интегральном исполнении в виде отдельных микросхем или непосредственно со схемой сумматора или арифметико-логического устройства в одной микросхеме.

Основными арифметическими операциями являются сложение и вычитание. Разработаны коды дополнительный и обратный, которые позволяют выполнять операцию вычитания методом суммирования. Для выполнения операции вычитания, при использовании дополнительного кода, вычитаемое следует перевести в дополнительный код и просуммировать с первым слагаемым. Полученный результат (разность) будет представлен в дополнительном коде. Затем его следует перевести в прямой код.

Прямой и дополнительный код положительных чисел совпадают. При преобразовании отрицательного числа в дополнительный код все разряды прямого кода следует проинвертировать и к младшему разряду добавить единицу. При обратном преобразовании дополнительного кода в прямой результат следует также проинвертировать и к младшему разряду добавить единицу.

Таким образом, выполнение операции вычитания методом суммирования требует дополнительных затрат времени и снижает быстродействие вычислительных средств.

Для повышения быстродействия ЭВМ разработаны и используются комбинированные арифметико-логические устройства, которые обеспечивают выполнение ряда арифметических и логических операций над прямыми кодами чисел без их преобразования.