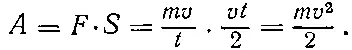Глеб Анфилов - Бегство от удивлений

К понятию энергии физика шла долго и трудно. Правда, о том, что движение не может пропасть бесследно или родиться из ничего, догадывались давно. Понимали это и Галилей, и еще более четко французский мыслитель Декарт, а за ним наш славный Ломоносов. Но то были слишком общие, чисто качественные, лишенные количественных оценок предположения.

Точность, математический символ, формула родились лишь в XIX столетии. Однако в узких рамках механики сохранение энергии (без употребления этого слова) было известно и Ньютону. Причем в соответствии с сугубо механическими истолкованиями силы (как причины ускорения тел), пути (обязательно в инерциальной системе отсчета), работы (произведения силы на путь). И отправным пунктом послужили-таки мысли о механической работоспособности. Как видите, здесь употреблен тот самый термин, который, как я уже говорил, в обычном, обывательском понимании далеко не всегда отвечает физической сущности энергии.

Сперва несколько простеньких выкладок.

Чтобы повесить у себя над столом портрет Ньютона, я забиваю гвоздь. Бью молотком по шляпке. Гвоздь лезет в стену.

На расстоянии, равном глубине (S) внедрения гвоздя, молоток прикладывает неизменную (это допускается ради простоты) силу F. Тогда при каждом ударе молоток, преодолевая сопротивление стены гвоздю, совершает работу, которая записывается так:

А = F·S.

Между тем, если верить второму закону Ньютона, сила измеряется произведением массы молотка на изменение его скорости во время удара. Это тоже легко записать математически. Пусть молоток, вгоняя гвоздь, затормозился от скорости v до полной остановки за время t. Тогда изменение его скорости (здесь не ускорение, а замедление, которое ради упрощения будем считать равномерным) составило: а = v/t , а сила F = mv/t

Поэтому на расстоянии S = at 2/2 = vt/2 была совершена работа

Эта работа выполнена за счет энергии движущегося молотка, которая, таким образом, равна этой же величине T= mv 2/ 2 — и называется кинетической энергией.

Только что добытая формула, выведенная Ньютоном, — целый рог изобилия научных откровений. По ней очень легко предсказывать, какую работу совершит движущееся тело, если его остановить. Пуля убивает волка, вода льется на лопасти турбины, брошенный камень сшибает с ветки яблоко — всюду затрачивается работа. И количество ее дается величиной Т. В этом смысле кинетическая энергия — действительно показатель механической работоспособности тела, «обещание» работы.

Напоминая вам эти школьные истины, скажу еще несколько слов о другом виде энергии — потенциальной.

Я живу в пятиэтажном доме на пятом этаже и горжусь этим. Потому что жильцы, обитающие на нижних этажах, по одному существенному признаку мне заметно уступают. Я гораздо богаче их именно потенциальной энергией.

Чем выше тело над земной поверхностью, тем больше затрачено работы на его подъем. Тяжелый чемодан поднять на пятый этаж труднее, чем легкий. А на третий этаж его поднять легче, чем на пятый. Значит, работа подъема П тут зависит от веса (обозначим его теперь через р) и от высоты подъема h:

П = ph.

А так как вес р равен массе m, помноженной на ускорение свободного падения g, то можно написать формулу:

П = mgh.

Такой величиной измеряется потенциальная энергия, иначе говоря, возможность движения, запасенная в поднятом теле: ведь истраченная работа не пропадает, а остается при чемодане в виде возможности упасть, скатиться, спуститься на веревке. В поднятом теле есть неиспользованная способность к движению, к скорости — значит, и к кинетической энергии. Так же, как в расслабленной руке есть неиспользованная способность совершить удар молотком. Слово «потенциал» в переводе с латыни означает «возможность». Это, как видите, не работа.

Это — запас работоспособности. Потенциальная энергия переходит в кинетическую, а та — в работу. И наоборот. Во всех движениях, где так или иначе совершается работа, происходят эти переливы.

Особенно легко их заметить во всевозможных аттракционах. Качели, гигантские шаги, спиральные спуски, лыжные трамплины — неплохие наглядные пособия для начинающих знатоков механики.

Когда речь заходит об энергии, популяризаторы да и ученые (вплоть до самого Эйнштейна) любят вспоминать аттракцион, который называется русскими горками.