Питер Эткинз - Десять великих идей науки. Как устроен наш мир.

расстояние 2= сторона 1 2+ сторона 2 2+ сторона 3 2 .

Мы не обязаны останавливаться на этом. Математики живут ненасытной страстью к обобщениям, и евклидова геометрия является богатой почвой для обобщений. Хотя большинство из нас не может вообразить что-нибудь за пределами наших домашних трех измерений, легко выразить свойства пространств больших размерностей, используя формулы. Так четырехмерная формула Пифагора будет иметь вид:

расстояние 2= сторона 1 2+ сторона 2 2+ сторона 3 2+ сторона 4 2 .

Вы могли бы подумать, что в размышлениях о пространствах с более высокими, чем три, размерностями мало пользы, если не считать интеллектуального удовольствия, но вы были бы неправы. Мы увидим, к примеру, что способность переходить из размерности в размерность является ценным способом изучения структуры нашего мира. Более того, можем ли мы быть уверены, что в нашем реальном мире имеются только три измерения, или есть несколько — даже много — других измерений, которые как-то спрятаны от нас? Мы видели в главе 8, что такой уверенности нет, так как, может быть, мы обитаем в десятимерном пространстве с дополнительным измерением в виде времени.

Я утверждал, что наше воображение не может выйти за пределы трех измерений. Это не вполне верно. Некоторые люди, потратившие в жизни много времени на изучение геометрий более высоких размерностей, заявляют, что имеют некоторое отдаленное представление о связях, существующих в четырех, а не в трех измерениях, и создают ошеломляющие компьютерные образы, изображающие трехмерные сечения четырехмерного, мира (рис. 9.1). [45]Я не призываю вас направить ваши умственные способности по этому пути, но для подготовки к тому, что последует дальше, мы нуждаемся в некотором знакомстве с четырехмерными ландшафтами. Чтобы осуществить это, мы должны вновь пройти фрагменты пути интеллектуальной революции, инициированной итальянскими художниками в конце тринадцатого, начале четырнадцатого веков, такими как Джотто ди Бондоне и Пьеро делла Франческа, которые начали передавать три измерения в двух, используя перспективу, математические основы которой заложил в конце восемнадцатого века Гаспар Монж, граф де Пелоуз (1746-1818) в своей Géométrie descriptive (1798). Затем мы должны пойти дальше и увидеть, как четырехмерные объекты могут быть представлены трехмерными изображениями в двумерных проекциях. Все это звучит довольно сложно, ибо это все равно что просить муравья, который всегда был заперт в плоском мире, воспользоваться своим воображением, чтобы представить себе еще и вертикаль. Но мы интеллектуально оснащены лучше, чем муравьи, и можем ожидать, что достигнем некоторого прогресса.

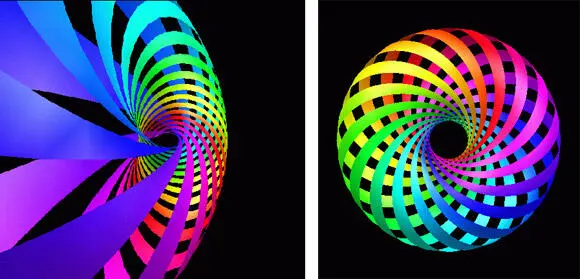
Рис. 9.1.Некоторое отдаленное представление об объектах в гиперпространстве может быть получено с помощью графических образов и анимаций. Здесь изображены два кадра анимации, изображающей вращение плоского тора в четырех измерениях, спроектированное в три измерения и затем представленное в двух.

Ноль-мерный куб (0-куб) — это точка. Представьте себе 0-куб как карандашную точку, тогда одномерный куб (1-куб) является линией, которую карандаш рисует, когда его двигают по прямой (рис. 9.2). Двумерный куб (2-куб) является плоской фигурой, порожденной протаскиванием 1-куба в новом направлении, лежащем перпендикулярно первому. Все это легко воспринять с помощью компаса нашего воображения, так же как и воображения смышленого муравья, и легко проделать на листе двумерной бумаги. Трехмерный куб (3-куб), заурядный повседневный куб, порождается протаскиванием плоского 2-куба в направлении, перпендикулярном его плоскости. С тем, чтобы вообразить этот шаг, проблем не возникает, хотя муравей был бы озадачен, поскольку ему не дано понять, как может существовать третье перпендикулярное направление. Не возникает проблем и с представлением 3-куба на 2-странице, обычном листе бумаги, поскольку мы теперь так хорошо знакомы с двумерными представлениями в искусстве, что расшифровываем эти представления без труда.

Рис. 9.2.Кубы различных размерностей могут быть построены с помощью движения куба предшествующей размерности в новом, перпендикулярном направлении. Здесь мы видим семейство кубов, построенных из 0-куба (точки). Отрезок (1-куб) получен протаскиванием точки в одном направлении, квадрат (2-куб) — протаскиванием отрезка в перпендикулярном направлении, обычный куб (3-куб) — протаскиванием квадрата в новом перпендикулярном направлении. Мы научились интерпретировать результаты двумерных представлений куба. Наконец, четырехмерный гиперкуб (4-куб) строится путем протаскивания 3-куба в еще одном перпендикулярном направлении. Мы, человеческие существа, еще не знаем, как интерпретировать результирующую диаграмму: я показываю два изображения, полученных вращением гиперкуба в разных направлениях.