Айзек Азимов - Популярная физика. От архимедова рычага до квантовой механики

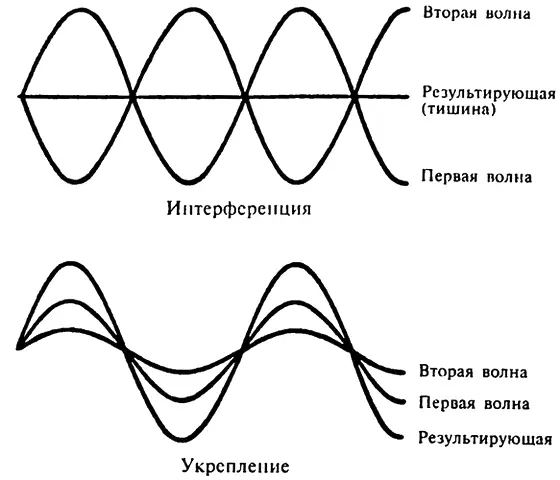
Давайте ограничимся рассмотрением очень простых примеров и не будем вовлекать сложные математические вычисления. Рассмотрим две ноты различной высоты тона, а потому — различной частоты, звучащие вместе. Сжатые области звуковой волны (или гребни, если мы будем говорить в более легко визуализируемых аналогиях поперечной волны) двигаются с более короткими интервалами — в случае ноты с более высокой частотой, а значит, они настигнут таковые звуковой волной с более низкой частотой.

Предположим, что одна нота имеет частоту 250 раз в секунду, а другая нота — частоту 251 раз в секунду, и предположим, что они начинают звучание в фазе. Первый гребень появляется одновременно у обеих нот. Второй гребень у ноты 251/с появляется только чуть-чуть раньше, чем второй гребень у ноты 250/с. Третий гребень появляется еще раньше, а четвертый гребень — раньше, чем третий. Однако в конце первой секунды и одна и другая ноты закончили точно 250 и 251 колебание соответственно. Они опять в фазе, но нота 251/с получает в каждую секунду один полный дополнительный гребень [54] Две ноты «гоняются друг за другом» только с точки зрения числа гребней, создаваемых в единицу времени, а не в смысле скорости. Обе ноты распространяются в пространстве с одной и той же скоростью. В действительности скорость звука не зависит от частоты. . И за каждую следующую секунду нота 251/с получает еще один новый дополнительный полный гребень.

В точке, где две ноты находятся в фазе, гребень к гребню, имеется короткий период полного укрепления, и нота звучит громко. По мере прохождения секунды и падения гребней они все более и более выходят из фазы, то есть интерференция все более и более увеличивается, а звук становится более тихим. В полуминутной точке, на полпути между двумя синфазными периодами, ноты полностью выходят из фазы и гребень одной располагается напротив впадины другой ноты; в этой точке имеется короткий период полной интерференции. Результатом ее является полное затухание и пропадание звука, причем периодичность затухания происходит с интервалом, следующим за тем, когда гребни совпадают. Такое периодическое изменение громкости, когда две ноты звучат вместе, называется «биением».

Давайте рассмотрим еще две ноты с частотами 250/с и 252/с соответственно. Тогда после половины секунды одна нота закончит 125 колебаний, а другая — 126 колебаний, и они возвратятся в фазу, соответствующую гребню. Это будет повторяться каждую половину секунды, то есть будут получаться два биения в секунду. Число биений в секунду, в случае одновременного звучания двух нот, равно разности в частоте этих двух нот.

Если биения настольно редкие, что их можно различимо услышать, то они создают звуковые комбинации, неприятные для слуха. Наиболее неприятным является, очевидно, 30 биений в секунду. Однако в том случае, когда число биений в секунду больше 60, они взаимопроникают друг в друга, и для человеческого уха их комбинация кажется приятной или гармоничной.

Теперь давайте рассмотрим две ноты, у которых одна имеет частоту точно в два раза больше другой. Например, первая имеет частоту 220/с, а вторая — 440/с; отношение частот равно 1:2. Число биений, когда ноты звучат вместе, равно 440—220, или 220 раз в секунду. Биения дублируют ноту более низкого тона, так что кажется, что две ноты «сплавляются» друг с другом и начинают представлять собой одну и ту же ноту. Они гармонируют друг с другом.

Именно Пифагор был первым, кто заметил, что гармонирующие ноты связаны между собой целочисленными отношениями небольшой величины. У него не было никакой аппаратуры для непосредственного измерения самой частоты, но он рассмотрел струны различной длины. Он обнаружил, что две струны с длинами, относящимися как 1:2, производят приятную комбинацию, так же как струны с соотношением длин 2:3 и 3:4.

(Результаты этих наблюдений за звуком были истолкованы Пифагором с мистической точки зрения. Он рассматривал роль взаимодействия небольших целочисленных отношений в создании благозвучий в соответствии со своими взглядами о том, что вся Вселенная управляется числами. Он и его ученики предполагали, что и сами планеты способны создавать звуки — так называемую «музыку сфер», ноты в которой основаны на их расстояниях относительно Земли. Наука не могла освободиться от этих заблуждений в течение 2000 лет.)