Поскольку пуаз слишком велик, чтобы быть удобным, когда мы имеем дело с большинством жидкостей, то для удобства используют сантипуаз (размером в одну сотую долю пуаза) и даже миллипуаз (размером в одну тысячную долю пуаза). Таким образом, вязкость воды при комнатной температуре равна примерно одному сантипуазу. При той же самой температуре вязкость диэтилового эфира (обычный обезболивающий препарат) равна 0,23 сантипуаза, или 2,3 миллипуаза, в то время как вязкость глицерина равна приблизительно 1500 сантипуазам, или 15 пуазам.
Движение жидкости оказывает влияние на ее давление. Вообразите столб воды, текущей через горизонтальную трубку некоего данного диаметра. Вода находится под давлением, иначе она бы не перемещалась, и давление (сила на единицу площади) — одно и то же во всех точках, поскольку вода течет с одной и той же скоростью во всех пунктах. Это можно продемонстрировать, если проткнуть трубку через некоторые интервалы и вставить в каждое отверстие еще одну трубку. В каждой трубке вода поднимется на один и тот же уровень.
Но предположим, что трубка имеет в середине некую сжатую область. Тот же самый объем воды был бы должен пройти через сжатую область за то же самое время, что и через равную длину несжатой области. Если бы этого не было, то вода накопилась бы на входе в сжатую область, чего, конечно, не происходит. (Если бы сжатие было достаточно узкое, чтобы перекрыть поток в целом, то поток бы остановился, и объем воды, проходящей через данное сечение, был бы равен 0 см 3/с — одинаково в сжатых и несжатых областях.)
Но для того чтобы один и тот же объем воды прошел через сжатые и несжатые области за данное время, поток воды должен быть более быстрым при прохождении через сжатую область (подобно тому, как широкая, медленно текущая река становится бурным потоком при прохождении через узкое ущелье). Так как при прохождении через узкую область скорость воды увеличивается, это показывает на ускорение и соответственно это должно быть вызвано силой. Мы можем достаточно легко найти такую силу, основываясь на разности в давлении. Если давление в несжатой части больше, чем в сжатой части, то имеется результирующая сила, направленная от несжатой части (высокое давление) к сжатой части (низкое давление), и жидкость действительно ускоряется в то время, как входит в сжатие.
Далее, когда жидкость оставляет сжатие и входит в новую несжатую область, ее скорость снова должна уменьшиться. Это снова показывает на ускорение, а значит, чтобы вызвать такое замедление скорости, должна существовать сила, направленная против потока. Однако поскольку новая несжатая область снова является областью высокого давления, такую силу можно выявить.
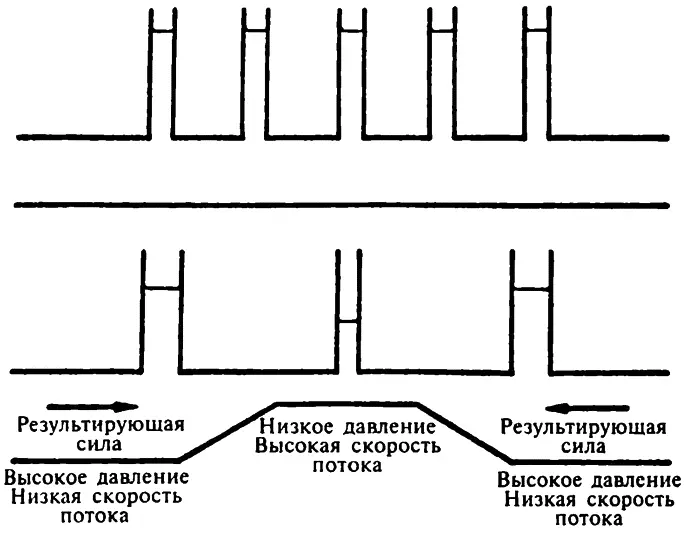
Принцип Бернулли
Короче говоря, все это можно выразить в виде некоего важного обобщения, что давление жидкости (или жидкость вообще) падает по мере увеличения ее скорости. Это называется принципом Бернулли, названным так в честь швейцарского математика Даниила Бернулли (1700–1782), который был первым, кто изучил данное явление в 1738 году и кто при изучении данного феномена изобрел термин «гидродинамика».
Свойства жидкости, описанные в предыдущей главе, являются весьма важными в связи с фундаментальным вопросом рассмотрения структуры строения материи — вопросом, который больше всего волновал ученых уже во времена древних греков.
Насколько можно видеть невооруженным глазом, материя может быть разделена на части неопределенное количество раз. Частичка бумаги может быть порвана пополам, на четверть, на восемь частей — и все еще оставаться бумагой. Капля воды может быть разделена на две меньшие капли или на четыре еще меньшие капли — и все еще оставаться водой. Может ли такое деление продолжаться вечно? Действительно ли материя непрерывна даже в своей окончательной малости? Так как не имелось никакой технической возможности, при помощи которой древние мыслители могли бы проверить это практическим путем, они обратились к логическим аргументам, основанным на том, что они считали первыми принципами.
Некоторые философы, особенно Демокрит из Абдерры (V столетие до н.э.), поддерживали ту точку зрения, что материя не может быть разделена вечно навсегда, что в конечном счете можно достигнуть некоторой очень маленькой части, которую уже невозможно будет далее разделить. Такую частицу материи он назвал «atomos» (в буквальном переводе — «неделимая часть»), и теперь мы говорим о его взглядах, что они представляют «атомизм», или «теорию атома».
Читать дальше













