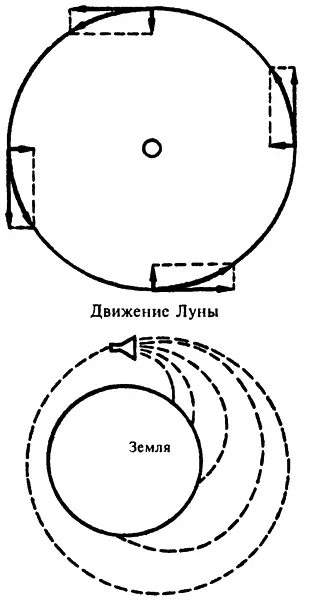
«На орбите»
При рассмотрении движения Луны мы должны учитывать только ту составляющую движения, которая направлена к Земле. Естественно возникает вопрос: не является ли этот компонент результатом действия той же силы, которая притягивает к земле яблоко? Ну что же, давайте обратимся к яблоку и посмотрим, как интерпретировать силу взаимодействия между ним и землей в свете законов движения.
Во-первых, все яблоки падают с одним и тем же ускорением, независимо от того, насколько они массивны. Но если одно яблоко имеет массу вдвое большую, чем второе яблоко, и все же падает с тем же самым ускорением, то на первое яблоко должна воздействовать вдвое большая сила (согласно второму закону движения). Сила, притягивающая яблоко к земле (часто ее называют весом яблока), должна быть пропорциональна массе яблока.
Но согласно третьему закону движения всякий раз, когда одно тело прикладывает силу к другому, второе прикладывает равную и противоположную силу к первому. Это означает, что, если Земля привлекает яблоко с некоторой нисходящей силой, яблоко привлекает Землю с равной восходящей силой.
Это кажется странным. Как крошечное яблоко может проявлять силу, равную той, что проявлена огромной Землей? Если бы это происходило, то можно было бы ожидать, что яблоко притянет к себе другие объекты, как это делает Земля, но этого, конечно, не происходит. Логично было бы объяснить это предположением, что сила притяжения между яблоком и землей зависит не только от массы яблока, но также и от массы Земли. Она не может зависеть от суммы масс, поскольку, когда мы удвоим массу яблока, суммарная масса яблока и Земли остается примерно прежней, в то время как сила притяжения удваивается. Очевидно, что она должна зависеть не от суммы масс, а от произведения масс.
Если мы умножаем массы, маленькая масса оказывает столь же сильный эффект на конечное произведение, как и большая. Таким образом, результатом умножения малого количества a на огромное количество b является произведение ab. Если теперь мы удвоим a , оно становится равным 2a. Если мы умножаем его на b, произведение становится равным 2ab. Таким образом, при удвоении одного из двух множителей в умножении маленький множитель может удвоить произведение. И удвоение массы яблока удваивает размер силы между яблоком и Землей.
Что же касается притяжения яблоком какого-либо другого объекта обычного размера, оно существует, но столь мало заметно из-за того, что произведение масс этих объектов составляет ничтожно малую часть от произведения массы этого объекта и массы Земли. Сила притяжения между двумя объектами обычного размера соответственно меньшая, и, несмотря на то что такая сила существует, она настолько бесконечно мала, что никак не может обнаружить себя при нормальном состоянии вещей.
Так как Земля притягивает все материальные объекты к себе (даже газообразная атмосфера крепко привязана к планете благодаря силе тяготения), может показаться, что сила тяготения в любой форме порождается массой Земли. Однако Земля вовсе не должна быть вовлечена. Любые две массы должны взаимодействовать гравитационно, и если мы замечаем силу, только когда вовлечена Земля, то потому, что сама наша Земля — единственное тело в нашем окружении достаточно массивное, чтобы породить силу тяготения, достаточно большую, чтобы заявить нам о своем существовании.
Такова сущность вклада Ньютона. Он не открывал закон тяготения в том смысле, что все земные объекты привлечены к земле. (Эта ограниченная концепция, по крайней мере, столь же стара, как Аристотель, а слово «тяжесть» использовалось в этом смысле в течение многих столетий до Ньютона.) Ньютон указал на то, что все существующие массы притягивают другие массы, таким образом, притяжение Земли не является уникальным. Ньютон утверждал, что между любыми двумя материальными телами во Вселенной имеется гравитационное притяжение, его обобщение называется «универсальный закон всемирного тяготения», и прилагательное «универсальный» — наиболее важное слово в этом названии [17] Однако из каждого правила можно изобрести исключение. Если бы Земля была полой, то в пределах пустоты не имелось бы никакой суммарной силы тяготения. Тело, находящееся в пределах этой пустоты, не было бы притянуто Землей. Однако это — искусственно придуманное исключение, которое не имеет никакого практического значения; любое тело, которое является достаточно большим, чтобы иметь поле тяготения значительной величины, является слишком большим, чтобы сохранять такую полую структуру.
.
Читать дальше













