Кудрявцев Степанович - Курс истории физики

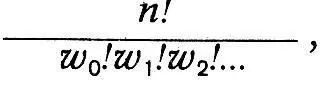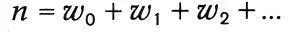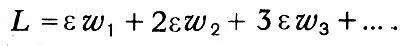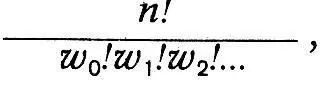
где n - общее число молекул, w0 - число молекул, обладающих энергией, равной нулю (Больцман считает энергию между 0 и ε, отступая от первоначальной квантовой гипотезы), w1, — число молекул, обладающих энергией ε (между ε и 2ε), и т. д. При этом

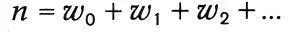
и общая энергия

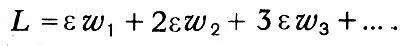
и общая энергия

Логарифмируя выражение для вероятности и определяя максимум этой логарифмической функции при условии постоянства n и L, Больцман находит распределение Максвелла — Больцмана, которое оказывается, таким образом, наиболее вероятным распределением. Подсчитывая наиболее вероятное распределение скоростей, Больцман вводит величину Θ, равную среднему логарифму функции распределения, взятой со знаком минус. Максимальное значение этой величины, которую Больцман называет «мерой распределения», при условии постоянства числа молекул и их общей кинетической энергии определяет наиболее вероятное распределение.

Величину, которую Больцман обозначал через Е и Θ, в дальнейшем стали обозначать Н, и она оказалась пропорциональной энтропии. Закон возрастания энтропии у Больцмана получает простую интерпретацию: «Система стремится к наиболее вероятному состоянию». Второе начало потеряло характер абсолютного закона природы и стало статистическим законом. В природе возможны процессы, происходящие в направлении убывания энтропии, и это, по мнению Больцмана, избавляет Вселенную от тепловой смерти. Для космоса в целом тепловой смерти нет. Взгляды и выводы Больцмана подвергались ожесточенной критике. Но вместе с тем они воспринимались и развивались другими исследователями: Максвеллом, Лоренцем, Планком. Планк дал простой вывод и простое точное выражение соотношения между энтропией и вероятностью. В обозначениях Планка оно имеет вид:

S = k lnW,

где S - энтропия, W - вероятность, k -постоянная, равная R/N, которую Планк назвал в честь Больцмана постоянной Больцмана. Из соотношения Планка исчезла неопределенная аддитивная константа, фигурирующая у Больцмана, и это соответствует тепловой теореме Нернста. формула соотношения между энтропией и вероятностью, данная Планком, фигурирует сегодня во всех руководства и монографиях как соотношение Больцмана.

В 1912 г., читая лекции по статистическим теориям термодинамики в Париже, Лоренц говорил об успехах кинетической теории газов. Он указывал, как бы подводя итоги многолетней борьбы сторонников феноменологического описания с приверженцами атомистики: «Теперь нельзя сомневаться в их существовании после того, как «реальность молекул» стала фактом, почти что «наблюдаемым» непосредственно; молекулы существуют для нас совершенно так Же, как и многие другие предметы, непосредственно нами не видимые, но в существовании которых наш ум вовсе не сомневается». Далее Лоренц продолжал: «Основываясь на этих блестящих результатах, можно поставить вопрос: нельзя ли найти закон Карно — Клаузиуса при помощи молекулярных теорий, понимая, конечно, последние в очень широком смысле, так как общности результата должна каким-либо образом соответствовать общность предпосылок? Австрийскому физику Больцману принадлежит честь первого успешного подхода к этой задаче и установление связи между понятием вероятности, определенным образом понимаемой, и термодинамическими функциями, в частности энтропией. Рядом с ним нужно считать одним из основателей этой новой ветви теоретической физики — статистической термодинамики — Уилларда Гиббса. Далее следует упомянуть работы Пуанкаре, Планка и Эйнштейна. Общий результат, который можно считать окончательно установленным, это существование связи между энтропией некоторого состояния и вероятностью этого состояния». К именам, упомянутым Лоренцем, следует добавить имена П.Эренфеста и Т. А. Афанасьевой-Эренфест, которым принадлежит ряд работ по статистической термодинамике, и в частности фундаментальная обзорная статья о принципиальных основах статистического понимания, опубликованная в «Математической энциклопедии» в 1911 г.

Все эти работы относятся к более позднему времени. Больцман же мог прочитать и оценить лишь книгу Гиббса «Основные принципы статистической механики», вышедшую в 1902 г. Он пришел также к пониманию идей Планка, как об этом писал сам Планк в своей автобиографии. Но все это происходило уже в XX в., когда физика переходила на новые пути, переживая мучительный кризис старого, «классического» понимания природы.